绝缘体的介电强度。计算示例

随着由电介质（绝缘体）隔开的导体（例如电容器板或导电电缆线）之间的电压 U 逐渐增加，电介质中电场的强度（强度）增加。电介质中的电场强度也随着导线之间的距离减小而增加。

在一定的场强下，电介质发生击穿，形成火花或电弧，电路中出现电流。绝缘发生击穿时的电场强度称为绝缘的电气强度Epr。

介电强度定义为每毫米绝缘厚度的电压，单位为 V/mm (kV/mm) 或 kV/cm。例如，光滑板之间空气的介电强度为 32 kV/cm。

当导体为由相等间隙分隔的板或条形式（例如，在纸电容器中）时，电介质中的电场强度通过以下公式计算

E = U / d，

其中 U 是导线之间的电压，V (kV)； d——介质层厚度，mm（cm）。

示例

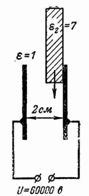
1. 如果板间电压 U = 100 kV（图 1），板间 3 cm 厚气隙中的电场强度是多少？

米。 1.

电场强度为：E=U/d=100000/3=33333V/cm。

这样的电压超过空气的介电强度（32 kV / cm）并且存在破坏的风险。

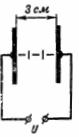
可以通过将间隙增加到例如 5 厘米，或使用其他更强的绝缘材料代替空气（例如电子纸板）来防止直流损坏的风险（图 2）。

米。 2.

电气纸板的介电常数为 ε = 2，介电强度为 80,000 V/cm。在我们的案例中，绝缘体中的电场强度为 33333 V。空气无法承受此力，而在本案例中的电气纸板具有 80,000/33333 = 2.4 的介电强度储备，因为电箱的介电强度为80,000/32,000 = 空气的2.5倍。

2. 如果电容器连接到电压 U = 6 kV，则 3 mm 厚电容器的电介质中的电场强度是多少？

E = U / d = 6000 / 0.3 = 20000 V / cm。

3. 厚度为 2 mm 的电介质在 30 kV 电压下击穿。它的电气强度是多少？

E = U / d = 30,000 / 0.2 = 150,000 V / cm = 150 kV / cm。玻璃具有这样的电气强度。

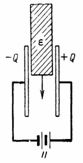
4. 电容器极板之间的空间填充有多层电气纸板和一层相同厚度的云母（图 3）。电容器极板之间的电压为 U = 10000 V。电子纸板的介电常数为 ε1 = 2，云母的介电常数为 ε2 = 8。绝缘层之间的电压 U 将如何分布，各层中的电场强度是多少？

米。 3.

相同厚度的介电层两端的电压 U1 和 U2 将不相等。电容器电压将分为电压 U1 和 U2，它们与介电常数成反比：

U1 / U2 = ε2 / ε1 = 8/2 = 4/1 = 4；

U1 = 4 ∙ U2。

由于 U = U1 + U2，我们有两个带有两个未知数的方程。

将第一个方程代入第二个：U = 4 ∙ U2 + U2 = 5 ∙ U2。

因此，10000 V = 5 ∙ U2； U2 = 2000 伏； U1 = 4，U2 = 8000V。

尽管介电层厚度相同，但它们的电荷并不相同。介电常数较高的电介质负载较小 (U2 = 2000 V)，反之亦然 (U1 = 8000 V)。

介电层中的电场强度 E 等于：

E1 = U1 / d1 = 8000 / 0.2 = 40,000 V / cm;

E2 = U2 / d2 = 2000 / 0.2 = 10000 V / cm。

介电常数的差异导致电场强度的增加。如果整个间隙只填充一种电介质，例如云母或电气纸板，电场强度会更小，因为它会相当均匀地分布在间隙中：

E = U / d = (U1 + U2) / (d1 + d2) = 10000 / 0.4 = 25000 V / cm。

因此，有必要避免使用具有非常不同的介电常数的复杂绝缘体。出于同样的原因，当绝缘层中形成气泡时，故障风险会增加。

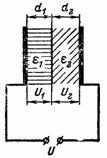
5. 如果介电层的厚度不同，则根据前面的示例确定电容器介电层中的电场强度。电气板的厚度 d1 = 0.2 mm，云母 d2 = 3.8 mm（图 4）。

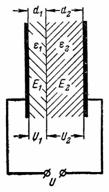
米。 4.

电场强度将与介电常数成反比分布：

E1 / E2 = ε2 / ε1 = 8/2 = 4。

由于 E1 = U1 / d1 = U1 / 0.2 和 E2 = U2 / d2 = U2 / 3.8，则 E1 / E2 = (U1 / 0.2) / (U2 / 3.8) = (U1 ∙ 3.8) / (0.2 ∙ U2) = 19 ∙ U1 / U2。

因此 E1 / E2 = 4 = 19 ∙ U1 / U2，或 U1 / U2 = 4/19。

介质层上的电压U1和U2之和等于电源电压U：U=U1+U2； 10000 = U1 + U2。

由于 U1 = 4/19 ∙ U2，则 10000 = 4/10 ∙ U2 + U2 = 23/19 ∙ U2； U2 = 190,000 /23 = 8260 V； U1 = U-U2 = 1740V。

云母中的电场强度为 E2 ∙ 8260 / 3.8≈2174 V / cm。

云母的电气强度为80,000 V/mm，可以承受这样的电压。

电纸板中的电场强度为E1 = 1740 / 0.2 = 8700 V / mm。

电气纸板无法承受这样的电压，因为它的介电强度仅为 8000 V/mm。

6. 60,000 V 的电压连接到两块相距 2 cm 的金属板。确定空气间隙中的电场强度，以及空气和玻璃中的电场强度，如果间隙中有玻璃，则插入一块带有厚度为 1 厘米（图 5）。

米。 5.

如果极板之间只有空气，则其中的电场强度等于：E=U/d=60000/2=30000V/cm。

场强接近空气的介电强度。如果在间隙中引入1cm厚的玻璃板（玻璃介电常数ε2=7），则E1=U1/d1=U1/1=U1； E2=U2/d2=U2/1=U2； E1 / E2 = ε2 / ε1 = 7/1 = U1 / U2；

U1 = 7 ∙ U2; U1 = 60,000-U2； 8 ∙ U2 = 60,000； U2 = 7500 伏； E2 = U2 / d2 = 7500 伏/厘米。

玻璃中的电场强度为E2=7.5kV/cm，其抗电强度为150kV/cm。

在这种情况下，玻璃具有 20 倍的安全系数。

对于气隙，我们有： U1 = 60,000-7500 = 52500 V； E1 = U1 / d1 = 52500 V / cm。

在这种情况下，空气间隙中的电场强度大于第一种情况，没有玻璃。插入玻璃后，整个组合的强度比单独的空气要小。

当玻璃板的厚度等于导电板之间的间隙，即2厘米，因为缝隙中难免会有薄薄的气隙被扎破。

高压导体之间间隙的介电强度必须使用介电常数低且介电强度高的材料来加强，例如，ε = 2 的电气纸板。避免使用具有高介电常数的材料（玻璃，瓷器）和空气，必须用油代替。