加热元件的计算

为了确定加热元件线材的主要参数之一——直径 d、m (mm)，使用两种计算方法：根据允许的比表面功率 PF 和使用电流负载表。

允许的比表面功 PF= P⁄F,

式中 P 为电热丝的功率，W；

F = π ∙ d ∙ l——加热器面积，m2； l——导线长度，m。

按照第一种方法

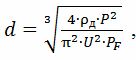
式中ρd——线材在实际温度下的电阻，Ohm•m； U为电热丝电压，V； PF——不同加热器的比表面功率允许值：

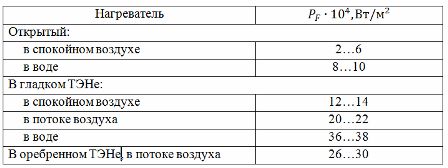
第二种方法使用根据实验数据编制的电流负载表（见表 1）。要使用所示表格，必须通过以下比率确定与导体实际（或允许）温度 Td 相关的计算加热温度 Tp：

Tr = Km ∙ Ks ∙ Td,

其中 Km 是安装系数，考虑到由于其结构而导致的加热器冷却条件的恶化； Kc 是环境因素，考虑到与静止空气环境相比加热器冷却条件的改善。

对于由螺旋形绞合线制成的加热元件，Km = 0.8 … 0.9；同样，陶瓷底座 Km = 0.6 ... 0.7；对于加热板和一些加热元件的导线 Km = 0.5 ... 0.6;对于来自电气地板、土壤和加热元件的导体，Km = 0.3 ... 0.4。 Km值越小对应的加热器直径越小，值越大对应的加热器直径越大。

当在非自由对流条件下运行时，Kc = 1.3 … 2.0 用于气流中的加热元件；对于静水中的元素，Kc = 2.5；在水流中 — Kc = 3.0 … 3.5。

如果设置未来（设计）加热器的电压 Uph 和功率 Pf，则其电流（每相）

Iph = Pph⁄Uph

根据表1计算出的发热体所需计算温度的发热体电流计算值，求出制造发热体所需的镍铬丝线径d和线材长度m计算：

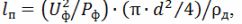
式中d为所选线径，m； ρd为导体在实际加热温度下的比电阻，Ohm•m，

ρd = ρ20 ∙ [1 + αp ∙ (Td-20)],

其中 αр — 电阻温度系数, 1/操作系统。

要确定镍铬螺旋线的参数，请取匝数的平均直径 D = (6 … 10) ∙ d，螺旋线的螺距 h = (2 … 4) ∙ d，

转弯数量

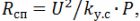
螺旋长度 lsp = h ∙ n。

在计算加热元件时，应记住螺旋线在加热元件后的电阻

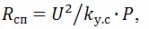
其中 k (y.s) 是考虑到螺旋阻力减小的系数；根据实验数据，k(s)=1.25。还应考虑到，螺旋线的比表面功率比管状加热元件的比表面功率大 3.5 ... 5 倍。

在加热元件的实际计算中，首先确定其表面温度Tp = To + P ∙ Rt1，

其中 为环境温度，°C； P为加热元件的功率，W； RT1——管道热阻——介质界面，ОC/W。

然后确定绕组的温度：Tsp = To + P ∙ (Rt1 + Rt2 + Rt3)，

式中Rt2为管壁热阻，ОC/W； RT3——填料的热阻，ОC/W； Rp1 = 1⁄ (α ∙ F)，其中α为传热系数，W / (m ^ 2 • ОС)； F——加热器面积，m2； Rt2 = δ⁄ (λ ∙ F)，其中δ为壁厚，m； λ——墙体的导热系数，W/(m•ОС)。

有关加热元件设备的更多信息，请参见此处： 加热元件。加热元件的装置、选择、操作、连接

表 1. 电流负载表

例1、根据许用比表面功率PF计算螺旋线形式的电加热器。

健康）状况。加热器功率P=3.5kW；电源电压 U = 220 V；电线材料 — 镍铬合金 Х20Н80（一种 20% 铬和 80% 镍的合金），因此电线的电阻率 ρ20 = 1.1 ∙ 10 ^ ( — 6) Ohm • m；电阻温度系数 αр = 16 ∙ 10 ^ (- 6) 1 /ОС；螺旋是开放的，呈金属形式，螺旋的工作温度为 Tsp = 400 ОC，PF = 12 ∙ 10 ^ 4 W / m2。确定 d、lp、D、h、n、lp。

回答。线圈电阻：R = U^2⁄P = 220^2⁄3500 = 13.8欧姆。

Tsp = 400 OS 时的比电阻

ρ400 = 1.1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (400-20)] = 1.11 ∙ 10 ^ (- 6) 欧姆•米。

求电线的直径：

从表达式 R = (ρ ∙ l) ⁄S 我们得到 l⁄d ^ 2 = (π ∙ R) ⁄ (4 ∙ ρ)，由此得出导线的长度

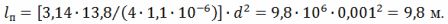
螺旋圈的平均直径为 D = 10 ∙ d = 10 ∙ 0.001 = 0.01 m = 10 mm。螺距 h = 3 ∙ d = 3 ∙ 1 = 3 mm。

螺旋圈数

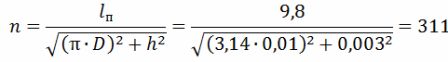
螺旋的长度为 lsp = h ∙ n = 0.003 ∙ 311 = 0.933 m = 93.3 cm。

示例 2. 使用电流负载表（参见表 1）确定线径 d 时，从结构上计算线电阻加热器。

健康）状况。加热丝功率P=3146W；电源电压 U = 220 V；线材 — 镍铬合金 Х20Н80 ρ20 = 1.1 ∙ 10 ^ ( — 6) Ohm • m; αp = 16 ∙ 10 ^ (- 6) 1 / ℃;位于气流中的开放螺旋线（Km = 0.85，Kc = 2.0）；导体的允许工作温度 Td = 470 ОС。

确定导线的直径 d 和长度 lp。

回答。

Tr = Km ∙ Ks ∙ Td = 0.85 ∙ 2 ∙ 470 OS = 800 OS。

设计加热器电流 I = P⁄U = 3146⁄220 = 14.3 A。

根据 Tр = 800 ОС 和 I = 14.3 A 时的电流负载表（见表 1），我们发现导线的直径和横截面 d = 1.0 mm 和 S = 0.785 mm2。

导线长度 lp = (R ∙ S) ⁄ρ800,

其中 R = U ^ 2⁄P = 220 ^ 2⁄3146 = 15.3 欧姆，ρ800 = 1.1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (800-20) ] = 1.11 ∙ 10 ^ (- 6) Ohm • m, lp = 15.3 ∙ 0.785 ∙ 10 ^ (- 6) ⁄ (1.11 ∙ 10 ^ (- 6)) = 10.9 m。

此外，如有必要，与第一个示例类似，可以定义 D、h、n、lsp。

例3.确定管式电加热器的允许电压（十）。

条件... 加热元件的线圈由镍铬合金线制成，直径 d = 0.28 mm，长度 l = 4.7 m。加热元件处于温度为 20 °C 的静止空气中。镍铬合金的特性： ρ20 = 1.1 ∙ 10 ^ (- 6) Ohm • m； αр = 16 ∙ 10 ^ (- 6) 1 / °C。加热元件外壳活动部分的长度为 La = 40 cm。

加热元件光滑，外径 DOB = 16 毫米。传热系数α=40W/(m^2∙°C)。热阻：填料 RT3 = 0.3 ОС / W，外壳壁 Rт2 = 0.002 ОС / W。

确定可以施加到加热元件上的最大电压是多少，使其线圈温度 Tsp 不超过 1000 ℃。

回答。加热元件的加热元件温度

Tsp = To + P ∙ (Rt1 + Rt2 + Rt3),

其中 是环境空气温度； P为加热元件的功率，W； RT1——管道-介质界面的接触热阻。

加热元件的功率 P = U ^ 2⁄R，

其中 R 是加热线圈的电阻。因此，我们可以写成 Tsp-To = U ^ 2 / R ∙ (Rt1 + Rt2 + Rt3)，由此加热元件上的电压

U = √ ((R ∙ (Tsp-To)) / (Rt1 + Rt2 + Rt3))。

求出 R = ρ ∙ (4 ∙ l) ⁄ (π ∙ d ^ 2)，

其中 ρ1000 = ρ20 ∙ [1 + αp ∙ (T-20)] = 1.1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (1000-20)] = 1.12 ∙ 10 ^ ( — 6) 欧姆 • 米。

那么 R = 1.12 ∙ 10 ^ (- 6) ∙ (4 ∙ 4.7) ⁄ (3.14 ∙ (0.28 ∙ 10 ^ (- 3)) ^ 2) = 85.5 欧姆。

接触热阻 RT1 = 1⁄ (α ∙ F),

其中F为发热体外壳活性部分的面积； F = π ∙ dob ∙ La = 3.14 ∙ 0.016 ∙ 0.4 = 0.02 m2。

求出 Rt1 = 1⁄ (40 ∙ 0.02 = 1.25) OC / W。

确定加热元件的电压 U = √ ((85.5 ∙ (1000-20)) / (1.25 + 0.002 + 0.3)) = 232.4 V。

如果加热元件上标明的标称电压为 220 V，则 Tsp = 1000 OS 时的过电压将为 5.6% ∙ Un。