计算电力负荷的系数
计算电网的任务是正确估计值 电气负载 以及分别选择最小的可能横截面的电线、电缆和汇流排，这些横截面将满足以下方面的标准化条件：
1.电热丝，
2.经济电流密度，
3. 网络各个部分的电气保护，
4.网络中的电压损失，
5.网络的机械强度。
导线截面选择的设计载荷为：
1.半小时最大I30-用于选择加热截面，
2. 平均开关负载 Icm——用于选择经济电流密度的截面，
3、峰值电流——用于熔断器的选择和过电流断路器的电流整定以及电压损失的计算。这种计算通常归结为确定在启动单个大功率鼠笼式电动机和无轨电车时供电网络中的电压损失。
在选择配电网的横截面时，无论受电设备的实际负载系数如何，都必须始终考虑满负荷使用的可能性，因此受电设备的额定电流必须为额定电流。只有选择不用于加热但用于过载扭矩的电动机电线允许例外。
因此，对于分销网络，结算本身不会发生。
为了确定供电网络中的估计电流，有必要找到许多能源消费者的最大或平均负载的组合，并且通常是不同的操作模式。因此，电力网络的计算过程相对复杂，分为三个主要的顺序操作：
1. 制定计算方案，
2.确定网络各个部分的组合最大负载或其平均值，
3.选段。
设计方案是在考虑电能分配时概述的供电概念的发展，必须包含有关连接负载、网络各个部分的长度以及所选类型和铺设方法的所有必要数据.
在大多数情况下，最重要的操作——确定网络各个部分的电力负载——是基于经验公式的使用。这些公式中包含的系数在很大程度上取决于电能消费者的操作模式，正确评估后者非常重要，尽管并不总是准确的。
同时，确定系数的不正确以及相应的负载可能导致网络带宽不足或整个安装价格的不合理增加。
在继续讨论确定电网电力负荷的方法之前，应注意计算公式中包含的系数并不稳定。由于技术的不断进步和自动化的发展，必须定期审查这些因素。
由于公式本身和其中包含的系数在一定程度上是近似的，需要注意的是，计算的结果只能是利息金额顺序的确定。因此，在算术运算中过于谨慎应该避免。
用于确定电气负载的计算公式中包含的值和系数
装机容量Ru表示：
1. 对于连续运行的电动机——目录（护照）中的标称功率，以千瓦为单位，由轴电机开发：
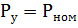
2. 对于间歇运行的电动机——标称功率降低到连续运行，即。到 PV = 100%：
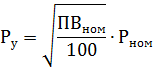
其中 PVN0M 是根据目录数据以百分比表示的额定占空比，Pnom 是 PVN0M 时的额定功率，
3、对于电炉变压器：
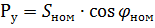
其中 СХ0М 是根据目录数据的变压器额定功率，kVA，cosφnom 是电炉在额定功率下运行的功率因数特性，
4. 对于焊接机器和设备的变压器——条件功率降低到连续运行，即。到 PV = 100%：
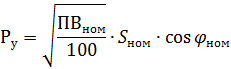
其中 Snom 是以千伏安为单位的变压器的占空比额定值，
在电动机的连接电源下，Ppr 被理解为电动机在额定负载和电压下从网络消耗的功率：
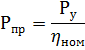
其中 ηnom 是以相对单位表示的电机额定功率。
最繁忙班次的平均有功负荷 Rav.cm 和相同的平均无功负荷 Qcp, cm 是系数除以最大负荷班次期间消耗的电量（分别为 WCM 和 VCM）除以班次持续时间（以小时为单位）Tcm，
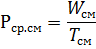
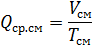
年平均有功负荷 Rav.g 和相同的无功负荷 Qcp.g 是年用电量（分别为 Wg 和 Vg）除以年工作时间（小时）（Tg）得到的系数：
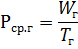
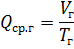
在最大负载下，Rmax 理解为一定时间间隔内的最大平均负载。
符合PUE，对于热网和变压器的计算，该时间间隔设置为 0.5 小时，即假设最大负载持续半小时。
辨别半小时最大负荷：有功P30，kW，无功Q30，kvar，满载S30，kVA和电流I30，a。
峰值电流 Ipeak 是给定电能消费者或一组电力消费者的瞬时最大可能电流。
在 KI 变化的利用率下，了解最大负载位移的平均有功负载与装机功率的比率：
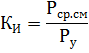
相应地，年利用率为年平均有功负荷与装机容量之比：
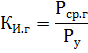
最大系数 Km 被理解为最大负载班次的有效半小时最大负载与平均负载的比率，
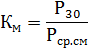
最大系数的倒数就是Kzap图的填充系数
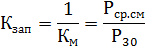
需求系数 Ks 为有效半小时最大负荷与装机容量之比：
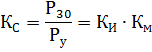
在包含因子下，Kv 被理解为一个轮班重复的短期和长期操作模式的接收者的工作时间与轮班持续时间的比率：
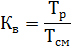
对于设计用于在切换期间连续操作的电接收器，切换因子实际上等于一。
有功功率负载系数K3是给定时间Pt受电设备的负载与装机功率之比：
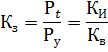
对于将装机功率理解为轴功率的电动机，将 Ki、Kv、K3 归因于连接到网络的电源而不是装机功率更为正确。
然而，为了简化计算，以及考虑到电机负载效率难以计算在内，建议这些因素也参考装机功率。因此，等于 1 的需求因数 (Kc = 1) 对应于电动机的实际负载，其量为满载的 η%。
最大负荷组合系数KΣ为若干组用电器的半小时最大负荷组合与各组最大半小时负荷之和的比值：
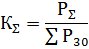
对于实际目的可接受的近似值，可以假设
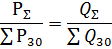
因此
