交流电路中的有源电阻和电感

考虑仅包含电感电阻的交流电路（参见文章 «交流电路中的电感器»)，我们假设该电路的有源电阻为零。

事实上，无论是线圈本身的导线还是连接导线都有一个很小但有源的电阻，所以电路不可避免地要消耗电流源的能量。

因此，在确定外电路的总电阻时，需要加上它的无功电阻和有源电阻。但是不可能将这两种性质不同的电阻相加。

在这种情况下，电路对交流电的阻抗是通过几何加法求得的。

构造一个直角三角形（见图1），其中一侧为感性电阻值，另一侧为有源电阻值。所需的电路阻抗由三角形的第三条边决定。

图 1. 确定包含电感和有源电阻的电路的阻抗

电路阻抗用拉丁字母 Z 表示，单位为欧姆。从构造中可以看出，总电阻总是大于单独取的电感和有源电阻。

总电路电阻的代数表达式为：

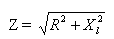
其中Z——总电阻，R——有源电阻，XL——电路的感性电阻。

因此，由有源电阻和感性电阻组成的电路对交流电的总电阻等于该电路的有源电阻和感性电阻的平方和的平方根。

欧姆定律 因为这样的电路由公式 I = U / Z 表示，其中 Z 是电路的总电阻。

现在让我们分析一下，如果电路除了电流和电感之间的相移之外，还有一个比较大的有源电阻，电压会是多少。在实践中，这样的电路可以是例如包含用细线绕制的铁芯电感器（高频扼流圈）的电路。

在这种情况下，电流和电压之间的相移将不再是四分之一周期（就像在只有电感电阻的电路中那样），而是更小；电阻越大，产生的相移越小。

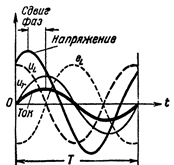
图 2. 包含 R 和 L 的电路中的电流和电压。

现在她自己 自感电动势 与电流源电压不反相，因为它相对于电压偏移不是半个周期，而是更少。另外，电流源在线圈两端产生的电压不等于自感电动势，而是比自感电动势大了线圈导线有源电阻的压降量。换句话说，线圈中的电压无论如何都由两个部分组成：

• tiL- 电压的无功分量，它平衡了自感应 EMF 的影响，

• tiR- 将克服电路有源电阻的电压的有源分量。

如果我们在线圈上串联一个大的有源电阻，相移会减小很多，电流正弦波几乎赶上电压正弦波，它们之间的相位差几乎看不出来。在这种情况下，项的振幅，并且将大于项的振幅。

同样，如果以某种方式降低发生器的频率，则可以降低相移，甚至将其完全降低为零。频率的降低将导致自感电动势的降低，因此导致电路中电流和电压之间的相移减小。

包含电感器的交流电路的功率

含有线圈的交流电路不消耗电流源的能量，电路中发电机与电路之间存在能量交换过程。

现在让我们分析一下这种方案消耗的功率会怎样。

交流电路中消耗的功率等于电流和电压的乘积，但由于电流和电压是可变量，那么功率也将是可变的。在这种情况下，如果我们将电流值乘以给定时刻对应的电压值，就可以确定每个时刻的功率值。

要得到功率图，我们需要将定义不同时间的电流和电压的直线段的值相乘。这种结构如图 1 所示。 3、一个。虚线波形 p 向我们展示了功率如何在仅包含电感电阻的交流电路中变化。

在构造这条曲线时使用了以下代数乘法规则：当一个正值乘以一个负值时，得到一个负值，当两个负值或两个正值相乘时，得到一个正值。

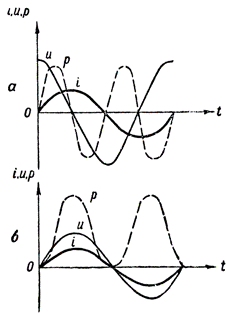
图 3. 功率图：a — 在包含电感电阻的电路中，b — 同样，有源电阻

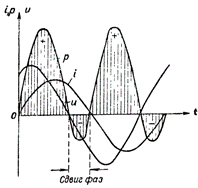
图 4. 包含 R 和 L 的电路的功率图。

在这种情况下，功率曲线位于时间轴上方。这意味着发电机和电路之间没有能量交换，因此发电机提供给电路的功率完全被电路消耗掉了。

在图。图 4 显示了包含电感和有源电阻的电路的功率图。在这种情况下，也会发生从电路到电流源的能量反向传输，但程度远低于具有单个电感电阻的电路。

查看以上功率图后，我们得出结论，只有电路中电流和电压之间的相移会产生“负”功率。在这种情况下，电路中电流和电压之间的相移越大，电路消耗的功率就越小，反之，相移越小，电路消耗的功率就越大。

另请阅读： 什么是电压谐振