电压、电阻和功率的三角形

对矢量图有想法的人都会很容易注意到，在它们上面可以非常清楚地分辨出一个直角电压三角形，每一边都反映了：电路的总电压、有源电阻的电压和电压 关于电抗.

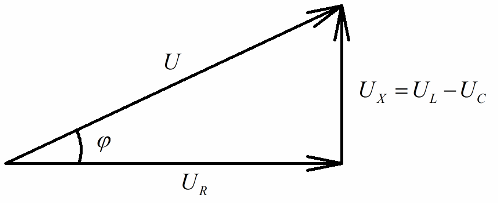
根据毕达哥拉斯定理，这些电压之间的关系（电路的总电压与其各部分的电压之间）将如下所示：

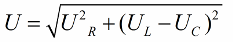
如果下一步是将这些电压的值除以电流（电流平均流过串联电路的所有部分），则由 欧姆定律 我们得到了电阻值，也就是说，现在我们可以讨论一个直角三角形的电阻：

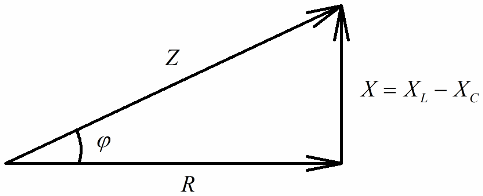
以类似的方式（如电压的情况），使用勾股定理，可以建立电路阻抗与电抗之间的关系。该关系将由以下公式表示：

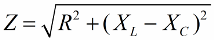
然后我们将电阻值乘以电流，实际上我们会将直角三角形的每一边增加一定的倍数。结果，我们得到一个直角三角形，其容量为：

在与电能的不可逆转换（在装置的工作性能中转化为热能）相关的电路有源电阻处释放的有功功率将明显与能量可逆转换（创造）中涉及的无功功率相关线圈和电容器中的磁场和电场），并为电气装置提供全功率。

有功功率以瓦特 (W) 为单位，无功功率以 varis（VAR — 无功伏安）为单位，总功率以 VA（伏安）为单位。

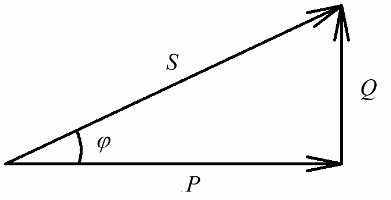
根据毕达哥拉斯定理，我们有权写：

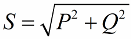
现在让我们注意一个事实，在功率三角形中有一个角 phi，其余弦值很容易主要通过有功功率和视在功率来确定。 这个角度的余弦值 (cos phi) 称为功率因数。它显示了在电气装置中做有用功时，总功率中有多少没有返回到电网。

显然，功率因数越高（最大值）表示输送到工厂运行的能量转换效率越高。如果功率因数为 1，则所有提供的能量都用于做功。

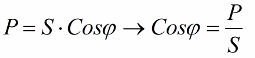
获得的比率允许根据功率因数、有功功率和网络电压来表达装置的电流消耗：

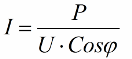
因此，余弦 phi 越小，网络完成某项工作所需的电流就越大。实际上，这个因素（最大网络电流）限制了传输线的传输容量，因此，功率因数越低，线路负载越大，可用带宽越低（低余弦 phi 导致限制）。电源线中的焦耳损耗随着余弦 phi 的减小可以从以下公式看出：

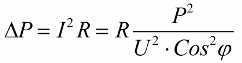
在传输线的有源电阻 R 上，电流 I 越大，损耗越大，即使它对负载无功。因此，我们可以说，功率因数低，输电成本只会增加。这意味着增加余弦φ是一项重要的国民经济任务。

理想的是总功率的无功分量应该接近于零。要做到这一点，最好总是满载使用电动机和变压器，并在使用结束时将它们关闭，以免它们闲置。空载时，电机和变压器的功率因数非常低。增加用户 cosine phi 的一种方法是使用 电容器组 和 同步补偿器.