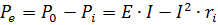电路中的功率平衡

根据 焦耳-楞次定律 直流电在电阻中所做的功，

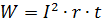
如果另一个将电磁能转换为机械能或化学能或其他形式的能量（电动机、充电电池等）的转换器代替电阻器包含在所考虑的支路中，则电流在时间 t 内所做的功可以计算为如果转换器电压已知的情况。

在这种情况下，Joule-Lenz 公式采用不同的形式：

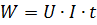
在直流电下，提供给电阻为 r 的电路部分的功率由以下表达式给出：

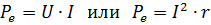
其中 I、U 和 r 保留与 Joule-Lenz 公式中相同的含义。

整个外电路消耗的功率和发电机提供的功率是一样的。发电机产生的功率总是大于发电机提供给外部电路的功率，因为​​一部分功率用于弥补发电机本身内部的损耗。

单个闭环的功率平衡表达式包含一个具有电动势 E 和内阻 ri 的发电机和一个电阻为 r 的电阻器，可以从基尔霍夫方程中获得。

对于这个电路

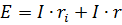
如果这个等式的两边都乘以电路中的电流，那么得到的等式将代表该电路中的功率平衡

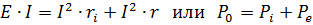
发电机产生的功率等于发电机内部损失并提供给外电路的功率之和。 P0=EI为发电机发出的功率，Pe=UI=I2r为发电机给外电路的功率，Pi—I2ri为发电机内部损失的功率。

当双端I流过的电流和双端U的电压选择相同的正方向时，两端消耗的功率，即产品的用户界面，必须为正。如果同时发现产品的用户界面为负，这将意味着具有两个端子的设备不消耗电磁能，相反，它是电磁能的发生器，并将该能量提供给 电路.

如果在电路中有多个具有两个端子的设备向电路发射电磁能，则其他设备会吸收该能量。在直流电路中，不会发生电磁能量的积累。因此，无源两端网络消耗的功率与发电机内部损失的功率之和必须等于所有发电机产生的功率的代数和，即在一个电路中工作的所有发电机的乘积 EkIk 的总和：

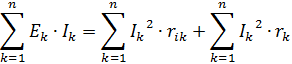
其中 n — 链中的分支数。

对于包含一个发电机的简单电路获得的平衡方程可以通过将外部电路中消耗的功率表示为发电机表示的功率和发电机内部损失的功率来重写：