感应电动机的功率因数——取决于什么以及它如何变化

在每台异步电动机的铭牌（铭牌）上，除其他运行参数外，其参数表示为 余弦 phi — cosfi… 余弦 phi 也称为感应电动机功率因数。

为什么这个参数叫做 cos phi？它与功率有什么关系？一切都很简单：phi 是电流和电压之间的相位差，如果绘制感应电机（变压器、感应炉等）运行过程中出现的有功功率、无功功率和总功率的图表，结果是比率有功功率到全功率的 - 这是余弦 phi - Cosphi，或者换句话说 - 功率因数。

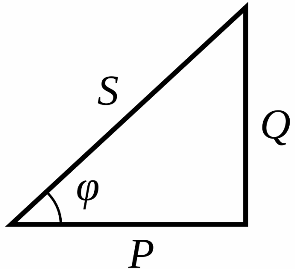
在额定电源电压和感应电机的额定轴负载下，余弦 phi 或功率因数将简单地等于其铭牌值。

例如，对于 AIR71A2U2 发动机，功率因数将为 0.8，轴负载为 0.75 kW。但此电机的效率为79%，因此电机在额定轴负载下消耗的有功功率将超过0.75 kW，即0.75 / Efficiency = 0.75 / 0.79 = 0.95 kW。

然而，在额定轴负载下，功率参数或 Cosphi 与网络消耗的能量精确相关。这意味着该电机的总功率将等于 S = 0.95 / Cosfi = 1.187 (KVA)。其中 P = 0.95 是电机消耗的有功功率。

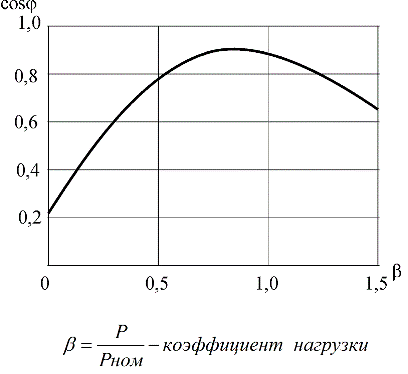
在这种情况下，功率因数或 Cosphi 与电机轴负载有关，因为轴机械功率不同，定子电流的有功分量也会不同。因此，在空闲模式下，即当轴上没有连接任何东西时，电机的功率因数通常不会超过 0.2。

如果轴负载开始增加，则定子电流的有功分量也将增加，因此功率因数将增加，在接近标称的负载下，功率因数约为 0.8 - 0.9。

如果现在负载继续增加，即给轴加载高于标称值，则转子将减速，增加 滑 s，转子的感应电阻将开始起作用，功率因数将开始下降。

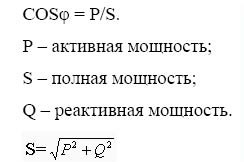
如果电机在一定时间段内空转，那么可以采取降低外加电压的方法，例如从三角形切换到星形，则绕组的相电压将降低 3 倍的根，来自空转转子的感性分量将减少，而定子绕组中的有功分量将略有增加。因此，功率因数会略有增加。

原则上，由交流电驱动的系统，如异步电动机，除了有源、感性和容性组件外，总是具有，因此，每半个周期，一定部分的能量返回到网络，即所谓的 无功功率Q. 

这一事实给电力供应商带来了问题：发电机被迫向电网提供全功率 S，电网返回发电机，但电线仍然需要合适的横截面来提供全功率，当然还有寄生热来自无功电流的电线来回循环......原来需要发电机提供全功率，其中一些基本没有用。

在纯有源形式下，发电厂的发电机可以为用户提供更多的电力，为此，功率因数必须接近于 1，即在 Cosphi = 1 的纯有源负载中。

为了保证这样的条件，一些大企业安装 无功补偿装置，即当功率因数降低时自动与异步电动机并联的线圈和电容器系统。

事实证明，无功能量在感应电机和给定装置之间循环，而不是在发电厂中的感应电机和发电机之间循环。因此，异步电动机的功率因数几乎达到 1。