磁路的欧姆定律

如果没有磁通量，现代电气工程就不可能存在。发电机和电动机、电磁铁和变压器、测量仪器和霍尔传感器的运行都是基于磁场的使用和磁通量的特性。

为了集中和加强磁通量，他们诉诸于使用铁磁材料。产生铁磁材料 磁芯 — 具有所需形状和尺寸的主体，用于将一种或另一种尺寸的磁通量导向所需方向的磁芯。这种磁感应闭合线在其内部通过的物体称为磁路。

磁场的已知特性使得计算各种磁路中的磁通量成为可能。但在实际工作中，求助于从磁场定律导出的一般推论和磁路定律，而不是每次都直接使用这些定律，要方便得多。将一定的规则应用于磁路，更便于解决典型的实际问题。

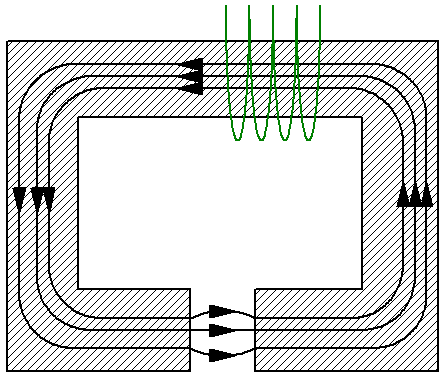
例如，考虑一个简单的磁路，它由横截面为 S 的无分支磁轭组成，而磁轭又由具有以下特性的材料制成 渗透率亩…磁轭有一个面积为 S 的非磁性间隙，例如空气，间隙中的磁导率 - mu1 - 与磁轭的磁导率不同。在这里，您可以查看平均感应线并将磁张力定理应用于它：

由于磁感应线在整个电路中是连续的，因此磁轭和间隙中的磁通量大小相同。现在我们使用公式 磁感应 B 和磁通量 F 以磁通量 F 表示磁场强度 H。

下一步是将所得表达式代入磁通量定理的上述公式：

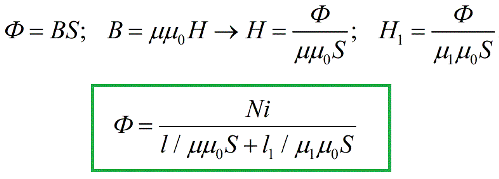
我们得到了一个与电气工程中已知的公式非常相似的公式 闭合电路部分的欧姆定律, 而电动势在这里的作用是由数量 iN 扮演的, 与电动势类比称为磁动势 (或 MDF)。在国际单位制中，磁动势的单位是安培。

分母中的和只不过是类比电路的总电阻，对于磁路则相应地称为总磁阻。分母中的项是磁路各个部分的磁阻。

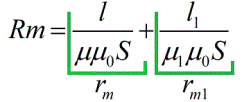
磁阻取决于磁路的长度、横截面积和磁导率（类似于通常的欧姆定律的电导率）。结果，您可以写出欧姆定律的公式，仅适用于磁路：

也就是说，与磁路相关的欧姆定律听起来像这样：«在没有分支的磁路中，磁通量等于 MDS 除以电路总磁阻的商。»

由公式可知，磁阻 在东北 以韦伯安培为单位测量，磁路的总磁阻在数值上等于该磁路各部分的磁阻之和。

所描述的情况适用于包含任意数量部件的无分支磁路，前提是磁通量依次穿过所有这些部件。如果磁芯是串联的，则总磁阻是通过将各部分的磁阻相加得出的。

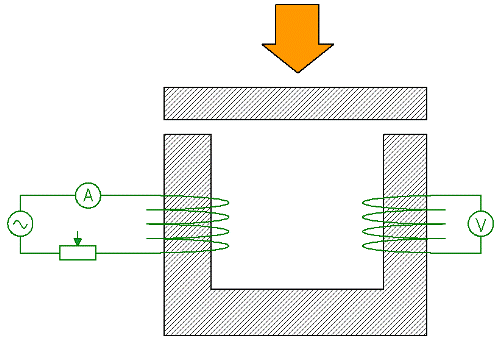
现在考虑一个演示电路各部分的磁阻对电路总磁阻影响的实验。U 形磁路由线圈 1 磁化，线圈 1 通过电流表和变阻器馈入（交流电）。在次级绕组 2 中感应出电动势，如您所知，连接到绕组的电压表的读数与磁路中的磁通量成正比。

如果现在用变阻器调节初级绕组中的电流不变，同时用铁片压住上面的磁路，当电路的总磁阻大大减小后，读数电压表将相应增加。

当然，上面的“磁阻”、“磁动势”等术语都是形式上的概念，因为磁通量中没有任何运动，也没有运动的粒子，它只是一种视觉表示（如流体流动模型）更清楚地了解法律...

上述实验和其他类似实验的物理意义是了解在磁路中引入非磁性间隙和磁性材料如何影响磁路中的磁通量。

例如，通过将磁铁引入磁路，我们向电路中已经包含的物体添加了额外的分子电流，从而引入了额外的磁通量。诸如《磁阻》和《磁动势》等正式概念在解决实际问题时被证明是非常方便的，这也是它们在电气工程中得到成功应用的原因。