变压器的主要特性

变压器的外部特性

众所周知，次级绕组两端的电压 变压器 取决于连接到该线圈的负载电流。这种依赖性称为变压器的外部特性。

变压器的外部特性在恒定电源电压下被去除，当负载发生变化时，实际上随着负载电流的变化，次级绕组端子处的电压，即变压器的次级电压也会发生变化。

这种现象的解释是，在次级绕组的电阻上，随着负载电阻的变化，电压降也会发生变化，并且由于初级绕组电阻两端的电压降的变化，EMF次级绕组相应变化。

由于初级绕组中的 EMF 平衡方程包含矢量，因此次级绕组两端的电压取决于负载电流和负载的性质：它是有源的、感性的还是容性的。

负载的性质由通过负载的电流与负载两端的电压之间的相位角值来证明。基本上，您可以输入一个负载系数，该系数将显示负载电流与给定变压器的额定电流相差多少倍：

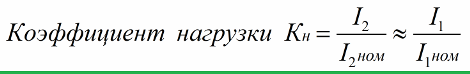
为了准确计算变压器的外特性，可以采用等效电路，通过改变负载电阻，可以固定次级绕组的电压和电流。

然而，以下公式在实践中证明是有用的，其中开路电压和以百分比测量的“二次电压变化”被替换并计算为开路电压与给定负载电压之间的算术差作为开路电压的百分比：

确定 «二次电压变化» 的表达式是根据变压器等效电路的某些假设获得的：

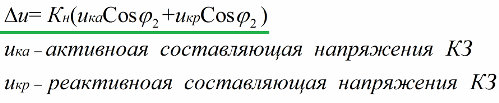
此处输入短路电压的无功分量和有功分量的值。这些电压分量（有源和无功）通过等效电路参数找到或通过实验找到 短路经验.

短路经历揭示了很多关于变压器的信息。短路电压是实验短路电压与额定初级电压的比值。 “短路电压”参数以百分比指定。

实验过程中，次级绕组与变压器短路，同时初级施加远低于额定值的电压，使短路电流等于额定值。这里，电源电压通过绕组两端的压降来平衡，施加的降低电压的值被认为是负载电流等于额定值时绕组两端的等效压降。

对于小功率电源变压器和电源变压器，短路电压值在5%～15%范围内，功率越大的变压器，该值越小。特定变压器的技术文件中给出了短路电压的准确值。

图中显示了根据上述公式构建的外部特性。我们可以看到图形是线性的，这是因为由于绕组电阻相对较低，次级电压对负载系数的依赖性不强，并且工作磁通量几乎不依赖于负载。

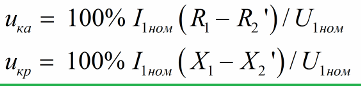
该图显示，根据负载的性质，相位角会影响特性曲线是下降还是上升。对于有源或有源电感负载，特性会下降，而有源电容负载会增加，然后“电压变化”公式中的第二项变为负数。

对于小功率变压器，有源元件通常比感性元件下降更多，因此有源负载的外部特性不如有源电感负载的线性。对于功率更大的变压器则相反，因此有源负载特性将更加严格。

变压器效率

变压器效率是输送到负载的有用电功率与变压器消耗的有功电功率之比：

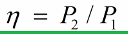
变压器消耗的功率是负载消耗的功率和变压器直接损耗的功率之和。此外，有功功率与总功率的关系如下：

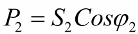
由于变压器的输出电压通常与负载的关系较弱，因此负载系数与额定视在功率的关系如下：

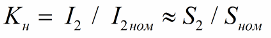
以及二次回路中负载消耗的功率：

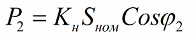
考虑到额定负载下的损耗，可以通过负载系数表示任意大小负载的电损耗：

标称负载损耗由短路实验中变压器消耗的功率非常精确地确定，磁性损耗等于变压器空载消耗的功率。这些损耗分量在变压器文档中给出。因此，如果我们考虑上述事实，效率公式将采用以下形式：

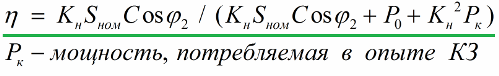
该图显示了变压器效率对负载的依赖性。当负载为零时，效率为零。

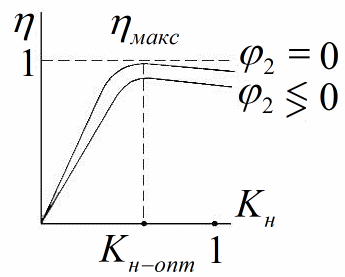
随着负载系数的增加，提供给负载的功率也随之增加，而磁损不变，效率呈线性增加，这是显而易见的。然后是负载因子的最佳值，效率达到极限，此时获得最大效率。

通过最佳负载系数后，效率开始逐渐下降。这是因为电损耗增加，它们与电流的平方成正比，因此与负载系数的平方成正比。大功率变压器（功率以kVA或以上为单位）的最大效率在98%~99%之间，小功率变压器（10VA以下）效率可达60%左右。

通常，在设计阶段，他们试图使变压器在最佳负载系数为 0.5 至 0.7 时效率达到最大值，然后在实际负载系数为 0.5 至 1 时，效率将接近其最大值。随着减少 功率因数（余弦 phi） 对于连接到次级绕组的负载，输出功率也降低，而电损耗和磁损耗保持不变，因此这种情况下的效率降低。

变压器的最佳运行模式，即 标称模式, 通常根据无故障运行条件和特定运行期间允许的加热水平进行设置。这是一个极其重要的条件，以便变压器在额定模式下运行时提供额定功率，而不会过热。