如何计算电感

正如力学中有质量的物体在空间中抵抗加速度，表现出惯性一样，电感阻止导体中的电流发生变化，表现出自感电动势。这是自感应的 EMF，它既反对电流的减少，试图维持它，也反对电流的增加，试图减少它。

事实是，在电路中电流变化（增大或减小）的过程中，该电流产生的磁通量也随之发生变化，主要局限在该电路所限定的区域内。并且随着磁通量的增加或减少，它会在同一个电路中感应出自感 EMF（根据楞次定律 - 与引起它的原因相反，即与开头提到的电流相反）。这里的电感 L 称为电流 I 与总磁通量 Φ 之间的比例因子，该电流由以下因素产生：

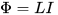
因此，电路的电感越高，它比产生的磁场越强，它阻止电流变化（它是产生它的磁场）因此电流通过更大的电感改变需要更长的时间，具有相同的施加电压。下面的说法也是正确的：电感越大，当通过电路的磁通量发生变化时，电路两端的电压就越大。

假设我们以恒定的速率改变某个区域的磁通量，然后通过用不同的电路覆盖这个区域，我们将在电感较大的电路上获得更大的电压（变压器，Rumkorf线圈等工作原理）。

但是环路电感是如何计算的呢？如何找到电流和磁通量之间的比例因子？首先要记住的是电感以亨利 (H) 为单位变化。在电感为 1 亨利的电路的端子处，如果其中的电流每秒变化 1 安培，就会出现 1 伏特的电压。

电感的大小取决于两个参数：电路的几何尺寸（长度、宽度、匝数等）和介质的磁性（例如，如果电路内部有铁氧体磁芯）线圈，它的电感会比里面没有铁芯的大）。

计算产生的电感，需要知道线圈本身会是什么形状，里面的介质会有多大的导磁率（介质的相对导磁率是真空的导磁率和磁导率的正比系数给定介质的渗透性。当然，不同的材料是不同的）...

让我们看一下用于计算最常见线圈形式（圆柱形螺线管、环形线圈和长线）的电感的公式。

这是计算电感的公式 螺线管 — 线圈，其长度远大于直径：

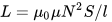
可以看到，已知匝数N、绕组长度l和线圈截面积S，我们求出线圈无芯或有芯的近似电感量，而磁真空的渗透率是一个常数值：

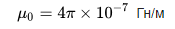
环形线圈的电感，其中 h 是环形线圈的高度，r 是环形线圈的内径，R 是环形线圈的外径：

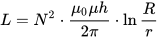
细线的电感（横截面的半径远小于长度），其中 l 是线的长度，r 是它的横截面的半径。指数为 i 和 e 的 Mu 是内部（内部，导体材料）和外部（外部，导体外的材料）环境的相对磁导率：

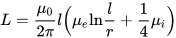
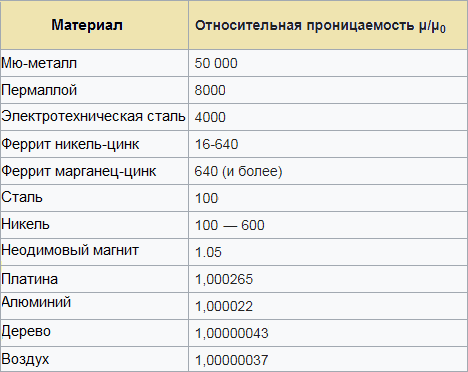
相对介电常数表将帮助您估算使用某种磁性材料作为磁芯的电路（电线、线圈）的电感值：