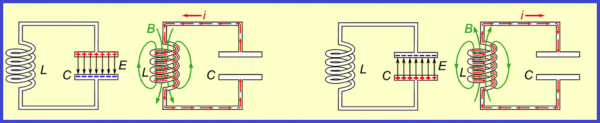
电磁振动——无阻尼和强迫振动

由电感器和电容器组成的电路中的电磁振动是由于电能与磁能的周期性转换而发生的，反之亦然。在这种情况下，电容器极板上的电荷和通过线圈的电流大小会周期性变化。

电磁振动是自由的和强制的。通常，自由振荡由于非零环路电阻而被阻尼，而强制振荡通常是自振荡。

获得 在振动电路中 自由振荡，我们首先需要使这个系统失去平衡：用初始电荷 q0 通知电容器或以某种方式启动电流脉冲 I0 通过线圈。

这将作为一种脉冲，电路中将发生自由电磁振荡 - 电容器通过感应线圈的交替充电和放电过程将开始，相应地，线圈磁场的可变上升和下降

由外部交变电动势在电路中维持的振荡称为强迫振荡。因此，正如您已经了解的那样，可以观察到自由电磁振荡的最简单振荡系统的示例是由电容 C 的电容器和电感 L 的线圈组成的振荡电路。

在真实的振荡电路中，电容器的充电过程会周期性重复，但振荡很快就会消失，因为能量主要消耗在线圈导线的有源电阻 R 上。

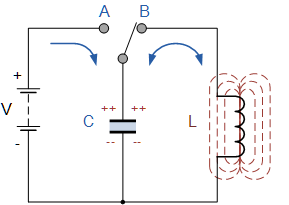
考虑一个具有理想振荡电路的电路。让我们首先用电池给电容器充电——我们将给它初始电荷 q0，也就是说，我们将用能量填充电容器。这将是电容器 We 的最大能量。

下一步是断开电容器与电池的连接，并将其与电感器并联。此时，电容器将开始放电，线圈电路中将出现增加的电流。电容器放电的时间越长，它逐渐进入线圈的电荷就越多，线圈中的电流就越大，因此线圈以磁场的形式储存能量。

这个过程不是瞬间发生的，而是逐渐发生的，因为线圈有电感，也就是说会出现自感现象，就是线圈无论如何都会抵抗电流的增加。在某一时刻，线圈的磁场能量达到最大可能值 Wm（取决于最初转移到电容器的电荷量以及电路的电阻）。

另外，由于自感现象，通过线圈的电流保持方向相同，但幅度减小，电荷最终再次积聚在电容器中。以这种方式，电容器被再充电。它的极板现在具有与实验开始时相反的电荷符号，当时我们将电容器连接到电池。

电容器能量已达到此电路的最大可能值。电路中的电流已停止。现在这个过程开始朝相反的方向发展，而且会一次又一次地继续，也就是说，会有自由的电磁振荡。

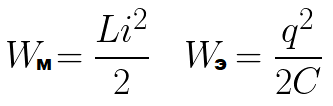
如果电路的有源电阻 R 等于零，则电容器板两端的电压和通过线圈的电流将根据谐波定律 - 余弦或正弦无限变化。这称为谐波振动。电容器板上的电荷也会根据谐波定律发生变化。

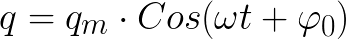
理想循环中没有损失。如果是，那么电路中的自由振荡周期将仅取决于电容器的电容 C 和线圈的电感 L 的值。可以使用 Thomson 公式找到这个周期（对于 R = 0 的理想循环）：

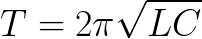
使用以下公式可以找到理想无损电路的相应频率和循环频率：

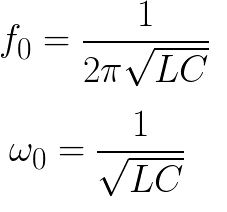
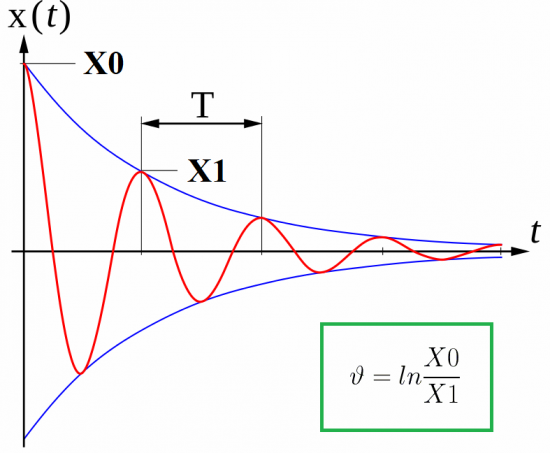
但理想的电路并不存在，并且电磁振荡会因电线发热造成的损耗而衰减。根据电路电阻 R 的值，每个后续的最大电容器电压将低于前一个。

针对这种现象，物理学中引入了振荡的对数衰减量或阻尼衰减量这样的参数。它被发现为振荡的两个连续最大值（具有相同符号）之比的自然对数：

对数振荡衰减通过以下关系与理想振荡周期相关，其中可以引入一个附加参数，即所谓阻尼因子：

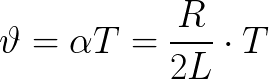
阻尼影响自由振动的频率。因此，计算实际振荡电路中自由阻尼振荡频率的公式与理想电路（考虑阻尼系数）的公式不同：

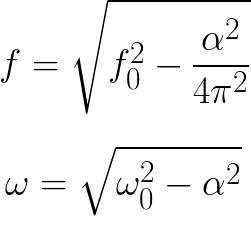
使电路产生振荡 取消静音，需要每半个周期补充和补偿这些损失。这是在连续振荡发电机中实现的，其中外部 EMF 源用其能量补偿热损失。这种具有外部 EMF 源的振荡系统称为自振荡。