电压谐振和电流谐振的应用

在电感 L、电容 C 和电阻 R 的振荡电路中，自由电振荡往往会衰减。为了防止振荡阻尼，有必要定期为电路补充能量，然后会发生强制振荡，这不会减弱，因为外部变量 EMF 已经支持电路中的振荡。

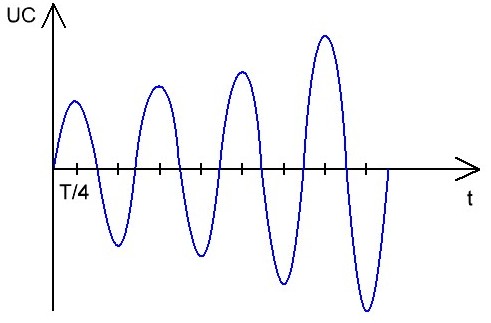
如果振荡由外部谐波 EMF 源支持，其频率 f 非常接近振荡电路 F 的谐振频率，则电路中电振荡 U 的幅度将急剧增加，即电谐振现象。

交流回路容量

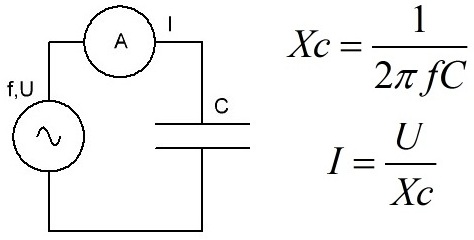
让我们首先考虑交流电路中电容器 C 的行为。如果在发电机上接一个电容器C，其两端的电压U按谐波定律变化，则电容器极板上的电荷将开始按谐波定律变化，类似于电路中的电流I .电容器的电容量越大，加在其上的谐波电动势的频率f越高，电流I就越大。

这个事实与所谓的想法有关电容XC的电容，它引入交流电路，起到限制电流的作用，类似于有源电阻R，但与有源电阻相比，电容不以热的形式耗散能量。

如果有源电阻消耗能量并因此限制电流，那么电容器限制电流仅仅是因为它没有时间存储比发电机在一个四分之一周期内所能提供的更多的电荷，而且，在下一个四分之一周期内，电容器将其电介质电场中积累的能量释放回发电机，也就是说，虽然电流有限，但能量没有耗散（我们将忽略电线和电介质中的损耗）。

交流电感

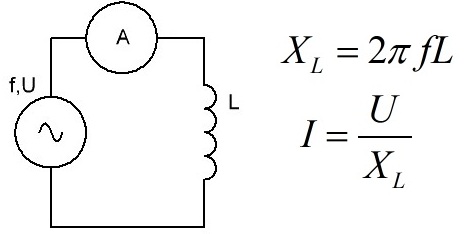
现在考虑交流电路中电感 L 的行为。如果不是电容器，而是电感 L 的线圈连接到发电机，那么当正弦波（谐波）EMF 从发电机提供到线圈的端子时，它将开始出现自感 EMF，因为当流过电感的电流发生变化时，线圈不断增加的磁场趋向于阻止电流的增加（楞次定律），即线圈似乎在交流电路中引入了一个电感电阻XL——除了导线电阻 R。

给定线圈的电感越大，发电机电流的频率 F 越高，电感电阻 XL 越高，电流 I 越小，因为电流根本没有时间稳定，因为自感的 EMF线圈会干扰它。并且每四分之一周期，储存在线圈磁场中的能量返回给发电机（我们暂时忽略导线中的损耗）。

阻抗，考虑到 R

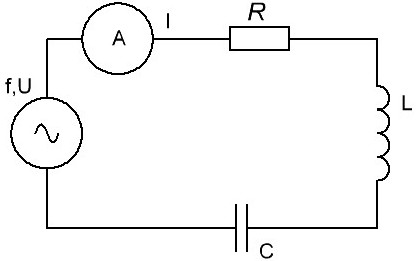
在任何实际的振荡电路中，电感L、电容C和有源电阻R都是串联的。

电感和电容在源的谐波电动势的每个四分之一周期内以相反的方式作用于电流：在电容器的极板上 充电时电压升高，虽然电流减小，但随着电流通过电感增加，电流虽然经历电感电阻，但增加并保持不变。

而在放电时：电容的放电电流最初很大，其极板上的电压趋于建立大电流，电感阻止电流增大，电感越大，放电电流越小。在这种情况下，有源电阻 R 引入纯有源损耗。也就是说，串联连接的 L、C 和 R 的阻抗 Z，在源频率 f 下，将等于：

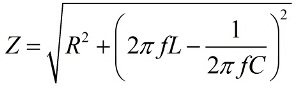
交流电的欧姆定律

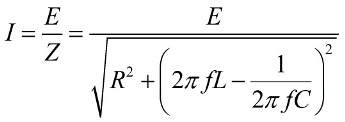
从交流电的欧姆定律可以明显看出，受迫振荡的振幅与 EMF 的振幅成正比并取决于频率。如果给定频率下的电感电阻和电容彼此相等，则电路的总电阻将最小，电流的幅度将最大，在这种情况下会发生谐振。振荡电路谐振频率的公式也由此推导出来：

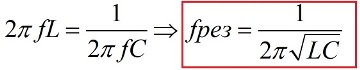
电压谐振

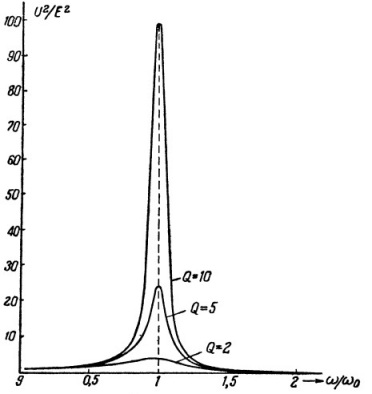
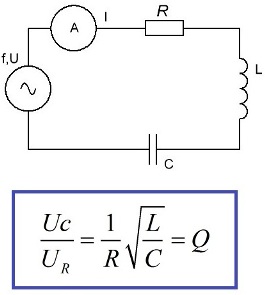
当电动势源、电容、电感和电阻相互串联时，这种电路中的谐振称为串联谐振或电压谐振。与电源的 EMF 相比，电压谐振的一个特征是电容和电感上的显着电压。

出现这样一幅画面的原因不言而喻。在有源电阻上，根据欧姆定律，会有一个电压Ur，在电容Uc上，在电感Ul上，将Uc与Ur作比后，我们就可以求出品质因数Q的值。电容两端的电压将是源电动势的 Q 倍，相同的电压将施加到电感上。

也就是说，电压谐振导致电抗元件上的电压增加 Q 倍，谐振电流将受到源的 EMF、其内阻和电路 R 的有源电阻的限制。因此，串联电路在谐振频率下的电阻最小。

应用电压谐振

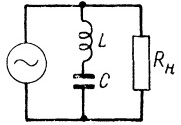
电压谐振现象用于 各种类型的电气滤波器例如，如果需要从发射信号中去除某一频率的电流分量，则在接收端并联一个电容和电感串联的电路，使得该谐振频率电流LC 电路将通过它闭合，它们不会到达接收器。

然后频率远离 LC 电路谐振频率的电流将不受阻碍地进入负载，只有频率接近谐振频率的电流才能找到通过 LC 电路的最短路径。

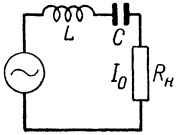
或相反亦然。如果只需要通过一定频率的电流，那么LC电路与接收器串联，则电路谐振频率的信号分量将几乎没有损耗地传递到负载，并且频率远离共振将显着减弱，我们可以说它们根本达不到负载。该原理适用于无线电接收器，其中调谐振荡电路被调谐以接收所需无线电台的严格定义的频率。

一般来说，电气工程中的电压谐振是一种不受欢迎的现象，因为它会导致过电压和设备损坏。

一个简单的例子是一条长电缆线，由于某种原因它没有连接到负载，但同时由中间变压器供电。这种带有分布电容和电感的线路，如果其谐振频率与供电网络的频率一致，就会被切断而失效。为防止电缆因意外谐振电压而损坏，需施加额外负载。

但有时电压共振会影响我们的利益，而不仅仅是收音机。例如，在农村地区，网络电压突然下降，机器需要至少 220 伏的电压。在这种情况下，电压谐振现象得以保存。

每相包括几个与机器串联的电容器就足够了（如果其中的驱动器是异步电动机），因此定子绕组上的电压将会升高。

这里重要的是选择正确数量的电容器，以便它们通过电容电阻和绕组的电感电阻精确补偿网络中的电压降，也就是说，通过稍微接近电路谐振，您可以增加即使在负载下的电压降。

电流谐振

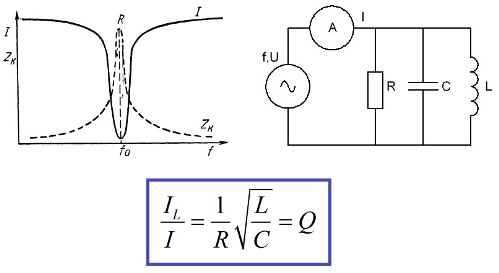
当电动势源、电容、电感和电阻相互并联连接时，这种电路中的谐振称为并联谐振或电流谐振。与源电流相比，电流谐振的一个特征是通过电容和电感的显着电流。

出现这样一幅画面的原因不言而喻。根据欧姆定律，通过有源电阻的电流将等于 U / R，通过电容 U / XC，通过电感 U / XL 并通过组成 IL 与 I 的比率，您可以找到品质因数的值Q. 通过电感的电流将是源电流的 Q 倍，相同的电流将每半个周期流入和流出电容器。

也就是说，电流的谐振导致通过电抗元件的电流增加 Q 倍，谐振电动势将受到电源电动势、其内阻和电路 R 的有源电阻的限制.因此，在谐振频率处，并联振荡电路的电阻最大。

谐振电流的应用

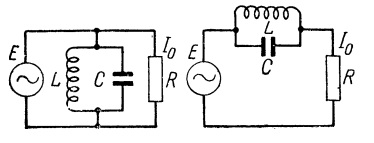
与电压谐振一样，电流谐振也用在各种滤波器中。但接上电路后，并联电路的作用与串联电路相反：与负载并联安装，并联振荡电路会使电路谐振频率的电流通过负载，因为电路本身的电阻在其自身的谐振频率下是最大的。

与负载串联安装，并联振荡电路不会传输谐振频率信号，因为所有电压都会落在电路上，负载会有一小部分谐振频率信号。

因此，电流谐振在无线电工程中的主要应用是在电子管发生器和高频放大器中为特定频率的电流产生大电阻。

在电气工程中，电流谐振用于实现具有显着电感和电容组件的负载的高功率因数。

例如， 无功功率补偿装置 (KRM) 是与在低于额定负载下运行的异步电动机和变压器绕组并联的电容器。

当设备的感应电阻等于网络频率下连接的电容器的容量时，精确地采用此类解决方案以实现电流谐振（并联谐振），从而使无功能量在电容器之间循环和设备，而不是设备和网络之间；因此电网仅在设备充电并消耗有功功率时才发射功率。

当设备不工作时，网络与谐振电路（外部电容器和设备的电感）并联连接，这代表了网络的非常大的复阻抗并允许减少 功率因数.