基本电量：电荷、电压、电流、功率、电阻

基本电气量：电流、电压、电阻和功率。

收费

电路中最重要的物理现象是运动 电荷……自然界中有两种电荷——正电荷和负电荷。就像电荷吸引一样，电荷排斥一样。这导致存在将等量的正电荷与负电荷分组的趋势。

原子由带负电的电子云包围的带正电的原子核组成。总负电荷的绝对值等于原子核的正电荷。因此，原子的总电荷为零，也称为电中性。

在可以容纳的材料中 电，一些电子从原子中分离出来，具有在导电材料中移动的能力。这些电子称为移动电荷或电荷载体。

由于初始状态下的每个原子都是中性的，带负电的电子分离后，变成带正电的离子。正离子不能自由移动并形成静止的固定电荷系统（参见 - 什么物质导电).

在半导体作为一类重要的材料，移动电子可以以两种方式移动：或者电子只是充当带负电的载体。或者许多电子的复杂集合以这种方式移动，就好像材料中有带正电的移动载流子一样。固定费用可以是任一性质。

导电材料可以被认为是包含移动电荷载体（可以具有两个符号之一）和相反极性的固定电荷的材料。

还有一些称为绝缘体的材料不导电。绝缘体中的所有电荷都是固定的。绝缘体的例子有空气、云母、玻璃、许多金属表面形成的薄层氧化物，当然还有真空（其中根本没有电荷）。

电荷以库仑 (C) 为单位测量，通常用 Q 表示。

通过大量实验确定了每个电子的电荷量或负电荷量，发现为 1.601 × 10-19 CL 或 4.803 × 10-10 静电荷。

即使在相对较低的电流下，也可以通过以下方式获得流过导线的电子数量的一些想法。由于电子的电荷量为1.601•10-19 CL，那么产生等于库仑电荷的电子数为给定的倒数，即约等于6•1018。

1 A 的电流对应于每秒 1 C 的电流，在通过导线横截面的电流仅为 1 μmka (10-12 A) 时，每秒大约有 600 万个电子。如此大的电流同时又如此之小，以至于它们的检测和测量与重大的实验困难有关。

正离子的电荷是电子电荷的整数倍，但符号相反。对于单个电离的粒子，电荷等于电子的电荷。

原子核的密度远高于电子的密度，整个原子占据的大部分体积是空的。

电现象的概念

通过将两个不同的物体摩擦在一起，以及通过感应，物体可以被赋予特殊的属性——电。这样的物体被称为带电的。

与带电体相互作用有关的现象称为 电现象.

带电体之间的相互作用由所谓的电力与另一种性质的力的不同之处在于，无论其运动速度如何，它们都会使带电物体相互排斥和吸引。

通过这种方式，带电物体之间的相互作用不同于引力相互作用，引力相互作用仅以物体的吸引力为特征，或者不同于磁源力，后者取决于电荷移动的相对速度，导致磁现象。

电气工程主要研究物性外在表现规律 带电体 ——电磁场定律。

电压

由于相反电荷之间的强烈吸引力，大多数材料都是电中性的。分离正电荷和负电荷需要能量。

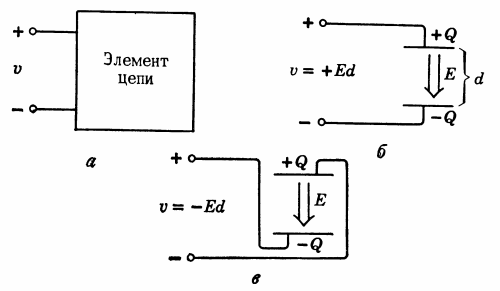
在图。图 1 显示了两个导电的、最初不带电的板，它们以距离 d 间隔开。假设板之间的空间充满绝缘体，例如空气，或者它们处于真空中。

米。 1. 两个导电的、最初不带电的板：a——板是电中性的； b——电荷-Q转移到底板（板间存在电位差和电场）。

在图。 1，两块板都是中性的，上板的总零电荷可以用电荷+Q和-Q的总和来表示。在图。如图 1b 所示，电荷 -Q 从上板转移到下板。如果在图1b，我们用导线连接极板，然后相反电荷的吸引力会导致电荷快速转移回来，我们将回到图 1b 所示的情况。 1，一个。正电荷将移动到带负电的板，而负电荷将移动到带正电的板。

我们说在图 1 所示的带电板之间。如图 1b 所示，存在电势差，带正电的上板电势高于带负电的下板电势。通常，如果两点之间的传导导致电荷转移，则两点之间存在电位差。

正电荷从高电位点移动到低电位点，负电荷移动方向相反——从低电位点到高电位点。

测量电位差的单位是伏特（V）。电位差称为电压，通常用字母 U 表示。

为了量化两点之间的张力，使用了这个概念 电场...在图所示的情况下。如图 1b 所示，在从较高电势区域（从正极板）到较低电势区域（到负极板）的极板之间存在均匀电场。

该场的强度以伏特/米表示，与板上的电荷成正比，如果已知电荷分布，则可以根据物理定律计算得出。电场大小与板间电压 U 之间的关系具有 U = E NS e（伏特 = 伏特 / 米 x 米）的形式。

所以，从低电势到高电势的转变对应于与场方向相反的运动。在更复杂的结构中，电场可能不是处处均匀的，为了确定两点之间的电势差，有必要反复使用等式 U = E NS e。

我们感兴趣的点之间的间隔被分成许多部分，每个部分都足够小以使得字段均匀分布在其中。然后将该等式连续应用于每个部分 U = E NS e 并且对每个部分的电位差求和。因此，对于电荷和电场的任何分布，您都可以找到任意两点之间的电势差。

测定电位差时，不仅要说明两点间电压的大小，还要说明哪一点的电位最高。然而，在包含多个不同元件的电路中，并不总是能够预先确定哪一点具有最高电位。为避免混淆，有必要接受标志的条件（图 2）。

米。 2…确定电压极性（电压可正可负）。

双极电路元件由配备两个端子的盒子表示（图 2，a）。假设从盒子到终端的线路是电流的理想导体。一个端子标有加号，另一个端子标有减号。这些字符固定了相对极性。图中的电压 U 2, 并且由条件 U = (端子 «+» 的电位) — (端子 «-« 的电位) 确定。

在图。在图 2b 中，带电板连接到端子，因此 «+» 端子连接到具有更高电位的板。这里电压U是正数。在图。 2、«+»端接下电位板。结果，我们得到一个负电压。

重要的是要记住应力表示的代数形式。一旦确定了极性，正电压意味着 «+» 端子具有（更高的电位），负电压意味着 «-» 端子具有更高的电位。

当前的

上面注意到正电荷载流子从高电位区移动到低电位区，而负电荷载流子从低电位区移动到高电位区。任何费用的转移都意味着到期 电.

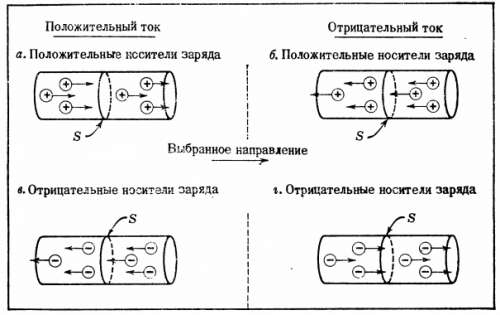
在图。图 3 显示了一些简单的电流流动情况，表面选择 C ​​并显示了名义上的正方向。如果随着时间 dt 通过 S 部分，总电荷 Q 将沿所选方向通过，则通过 S 的电流 I 将等于 I = dV/dT。电流的计量单位是安培（A）（1A=1C/s）。

米。 3…电流方向与移动电荷流动方向的关系。如果通过某个表面 C 的正电荷流与所选方向一致，则电流为正（a 和 b）。如果所产生的正电荷流过表面的方向与所选方向相反，则电流为负（b 和 d）。

在确定电流 Iz 的符号时经常会出现困难。如果移动电荷载流子是正的，那么正电流描述了移动载流子在所选方向上的实际运动，而负电流描述了移动电荷载流子与所选方向相反的流动。

如果移动运营商是负面的，则在确定电流方向时必须小心。考虑图。图 3d，其中负移动电荷载流子在所选方向上穿过 S。假设每个载流子都有电荷 -q 并且通过 S 的流速是每秒 n 个载流子。在 dt 期间，电荷 C 在所选方向上的总通过将是 dV = -n NS q NS dt，这对应于电流 I = dV/ dT。

因此，图 3d 中的电流为负。此外，该电流与带电荷 + q 的正载流子以每秒 n 个载流子的速度在与所选载流子相反的方向上通过表面 S 运动产生的电流一致（图 3，b）。因此，两位数的电荷反映在两位数的电流中。对于电子电路中的大多数情况，电流的符号很重要，并且载流子（正或负）携带该电流并不重要。因此，当他们谈论电流时，他们通常假设电荷载流子是正的（见—— 电流方向).

然而，在半导体器件中，正电荷载流子和负电荷载流子之间的差异对于器件的运行至关重要。对这些设备的操作进行详细检查应清楚地区分移动充电载体的迹象。电流流过某个区域的概念可以很容易地概括为流过电路元件的电流。

在图。图4显示双极元件。正电流的方向由箭头表示。

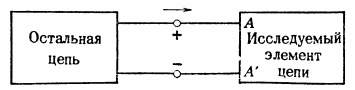
米。 4. 通过电路元件的电流。电荷以 i（每秒库仑数）的速率通过 A 端进入电池，并以相同的速率通过 A' 端离开电池。

如果正电流流过电路元件，则正电荷以每秒 i 库仑的速率进入端子 A。但是，如前所述，材料（和电路元件）通常保持电中性。 （即使图 1 中的“已充电”电池的总电荷为零。）因此，如果电荷通过端子 A 流入电池，则必须同时有等量的电荷通过端子 A' 流出电池。这种电流流过电路元件的连续性源于元件作为一个整体的中性。

力量

电路中的任何双极元件都可以在其端子之间产生电压，并且电流可以流过它。电流和电压的符号可以独立确定，但电压和电流的极性之间存在重要的物理关系，为了阐明这种关系，通常会采用一些附加条件。

在图。图 4 显示了如何确定电压和电流的相对极性。选择当前方向后，它会流入 «+» 端子。当满足这个附加条件时，就可以确定一个重要的电量——电功率。考虑图 1 中的电路元件。 4.

如果电压和电流为正，则正电荷从高电位点连续流向低电位点。为了保持这种流动，有必要将正电荷与负电荷分开并将它们引入 «+» 端子。这种连续分离需要持续消耗能量。

当电荷通过元素时，它们会释放这种能量。由于能量必须储存，它要么以热量的形式在电路元件中释放（例如，在烤面包机中），要么储存在其中（例如，在为汽车电池充电时）。这种能量转换发生的速率称为 力量 并由表达式 P = U NS Az（瓦特 = 伏特 x 安培）确定。

功率的计量单位是瓦特（W），相当于1焦耳的能量转化为1秒。功率等于电压和电流的乘积，极性如图 1 所示。 4是代数量。

如果 P > 0，如上述情况，功率会在元件中耗散或吸收。如果 P < 0，则在这种情况下，该元件为其连接的电路供电。

电阻元件

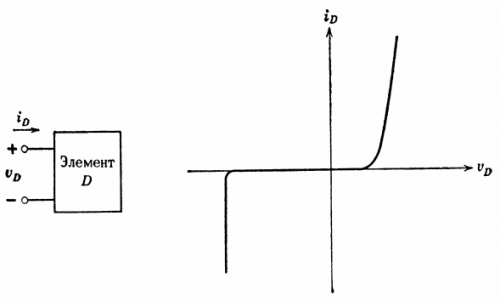
对于每个电路元件，您可以写出端电压与通过该元件的电流之间的特定关系。电阻元件是可以绘制电压和电流之间关系的元件，该图称为电流-电压特性。这种特征的一个例子如图 1 所示。 5.

米。 5.电阻元件的电流-电压特性

如果已知元件 D 端子处的电压，则该图可以确定通过元件 D 的电流。同样，如果电流已知，则可以确定电压。

完美抵抗

理想电阻（或电阻器）是 线性电阻元件…根据线性的定义，线性电阻元件中电压和电流之间的关系是这样的：当电流加倍时，电压也加倍。一般来说，电压应与电流成正比。

电压和电流之间的比例关系称为 电路部分的欧姆定律 并且有两种写法：U = I NS R，其中 R 是元件的电阻，I = G NS U，其中 G = I / R 是元件的电导率。电阻的单位是欧姆（ohm），电导率的单位是西门子（cm）。

理想电阻的电流-电压特性如图 1 所示。 6. 该图是一条通过原点的直线，斜率等于 Az/R。

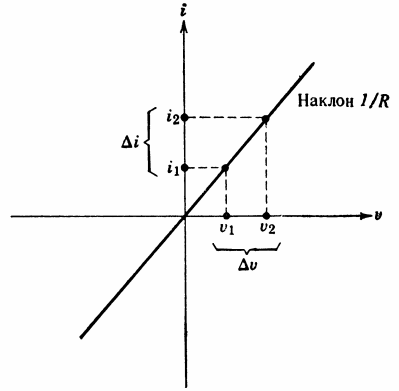
米。 6. 理想电阻器的名称 (a) 和电流-电压特性 (b)。

完美抵抗力

表示理想电阻吸收的功率：

P = U NS I = I2NS R, P = U2/ R

正如理想电阻中吸收的功率取决于电流（或电压）的平方一样，理想电阻中吸收的功率 v 的符号取决于 R 的符号。虽然有时使用负电阻值在模拟以特定模式运行的特定类型设备时，所有实际电阻通常都是正值。对于这些电阻，吸收功率始终为正。

电阻吸收的电能，acc 能量守恒定律, 必须 NS 转化为其他物种。大多数情况下，电能会转化为热能，称为焦耳热。排泄率 焦耳热 就电阻而言，它与电能的吸收率相匹配。例外是那些电阻元件（例如，灯泡或扬声器），其中部分吸收的能量被转换成其他形式（光能和声能）。

主要电气量的相互关系

对于直流电，基本单位如图 1 所示。 7.

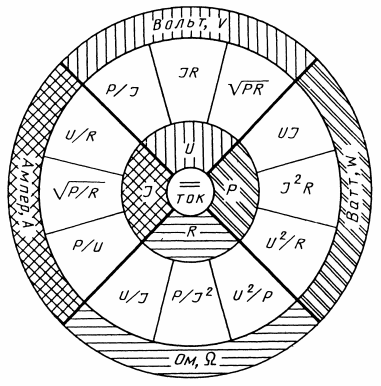
米。七、主要电气量的相互关系

四个基本单位——电流、电压、电阻和功率——通过可靠建立的关系相互连接，这使我们不仅可以进行直接测量，还可以进行间接测量，或者从其他测量值中计算出我们需要的值。因此，要测量电路中某一部分的电压，必须要有电压表，但即使没有电压表，只要知道电路中的电流和该部分的电流电阻，就可以计算出电压值。