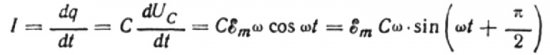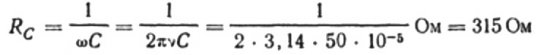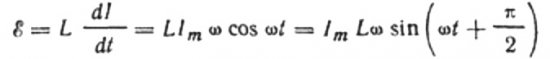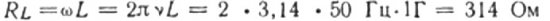交流电路中的容性和感性电阻

如果我们在直流电路中包括一个电容器，我们会发现它具有无限大的电阻，因为直流电根本无法通过板之间的电介质，因为根据定义，电介质不传导直流电。

电容器断开直流电路。但是如果现在把同一个电容加入到交流电路中，那么结果发现它的电容好像并没有完全坏掉，只是简单的交替充电，也就是电荷移动，外电路中的电流为保持。

在这种情况下，根据麦克斯韦理论，我们可以说电容器内部的交变传导电流仍然是闭合的，只是在这种情况下——通过偏置电流。这意味着交流电路中的电容器充当一种有限值电阻。这种阻力被称为 容性的.

长期以来的实践表明，流过导体的交流电流量取决于该导体的形状及其周围介质的磁性。直的导线，电流最大，同样的导线绕成匝数多的线圈，电流就小。

而如果在同一个线圈中引入铁磁芯，电流会下降得更多。因此，导线提供交流电不仅带有欧姆（有源）电阻，而且还带有附加电阻，具体取决于导线的电感。此电阻称为 归纳的.

其物理意义是在具有一定电感的导体中变化的电流会在该导体中引发自感电动势，该电动势趋于阻止电流的变化，即趋于减小电流。这相当于增加了导线的电阻。

交流电路中的电容

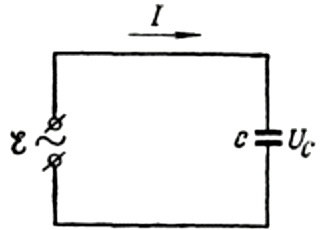
首先，让我们更详细地谈谈电容电阻。假设一个电容值为 C 的电容器连接到一个正弦交流电源，那么这个电源的电动势将由以下公式描述：

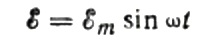
我们将忽略连接线上的电压降，因为它通常很小，必要时可以单独考虑。现在让我们假设电容器极板上的电压等于交流电源电压。然后：

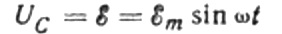
在任何给定时刻，电容器上的电荷取决于其电容和极板之间的电压。然后，给定上面提到的已知源，我们得到一个表达式，用于通过源电压找到电容器板上的电荷：

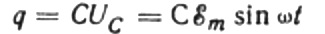
假设在无限小的时间 dt 内，电容器上的电荷变化量为 dq，则电流 I 将从电源流过电线流向电容器，等于：

当前幅度的值将等于：

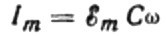
那么电流的最终表达式将是：

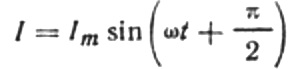
让我们重写电流幅度公式如下：

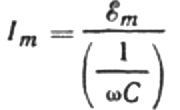
这个比值就是欧姆定律，其中角频率和电容的乘积的倒数起到电阻的作用，实际上是求正弦交流电路中电容器电容量的表达式：

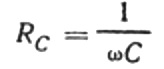
这意味着电容电阻与电流的角频率和电容器的电容成反比。这种依赖的物理意义很容易理解。

交流电路中电容器的电容越大，电路中电流的方向变化越频繁，最终每单位时间通过连接电容器和交流电源的导线横截面的总电荷就越多。这意味着电流与电容和角频率的乘积成正比。

例如，对于频率为50赫兹的正弦交流电路，我们计算一个电容量为10微法的电容器的电容量：

如果频率为 5000 Hz，则同一电容器将呈现大约 3 欧姆的电阻。

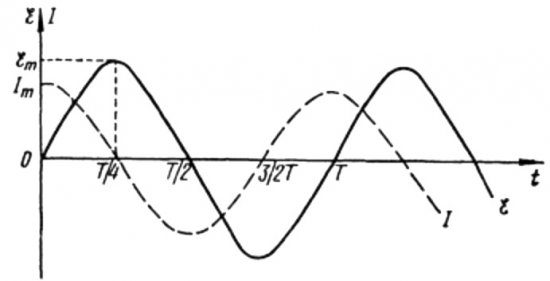
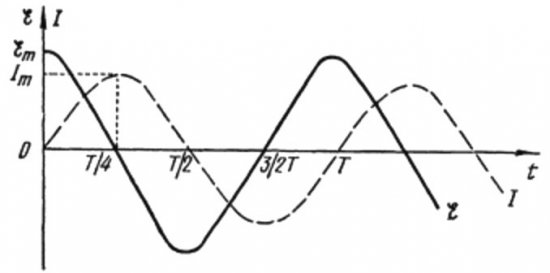
从上面的公式可以清楚地看出，在带有电容器的交流电路中，电流和电压总是以不同的相位变化。电流相位超前电压相位 pi / 2（90 度）。这意味着最大电流在时间上总是比最大​​电压早四分之一周期。因此，在电容电阻两端，电流超前电压四分之一的时间，或相位超前 90 度。

让我们解释一下这种现象的物理意义。在第一瞬间，电容器完全放电，因此施加在电容器上的最轻微电压已经移动电容器极板上的电荷，从而产生电流。

随着电容器充电，其板上的电压增加，这阻止了电荷的进一步流动，因此尽管施加到板上的电压进一步增加，但电路中的电流减少。

这意味着如果在初始时刻电流最大，那么当电压在四分之一周期后达到最大值时，电流将完全停止。

在周期开始时，电流最大，电压最小，开始增加，但经过四分之一周期后，电压达到最大值，但此时电流已经降为零。因此，事实证明电压超前电压四分之一的周期。

交流感应电阻

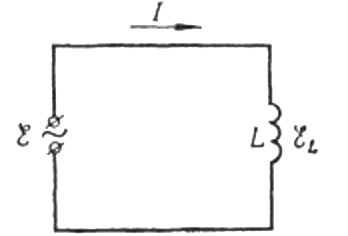
现在回到电感电阻。假设交变正弦电流流过电感线圈。可以表示为：

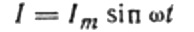
电流是由于施加到线圈的交流电压。这意味着线圈上会出现自感电动势，表示为：

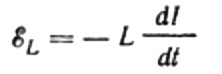
同样，我们忽略了将 EMF 源连接到线圈的电线上的电压降。它们的欧姆电阻非常低。

让在任何时刻施加在线圈上的交流电压完全被产生的自感电动势完全平衡，其大小等于它，但方向相反：

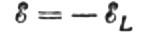
那么我们有权写：

由于施加到线圈的电压幅度为：

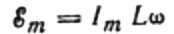
我们得到：

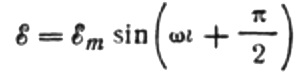
让我们将最大电流表示如下：

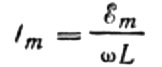
这个表达式本质上是欧姆定律。等于电感和角频率的乘积的量在这里起电阻的作用，无非就是电感器的电感电阻：

因此，电感电阻与线圈的电感和通过该线圈的交流电的角频率成正比。

这是由于感性电阻是由于自感电动势对电源电压的影响，-自感电动势倾向于减小电流，因此在电路中带来电阻。众所周知，自感电动势的大小与线圈的电感和通过线圈的电流变化率成正比。

例如，让我们计算电感为 1 H 的线圈的电感电阻，该线圈包含在电流频率为 50 Hz 的电路中：

如果球的频率为 5000 赫兹，则同一线圈的电阻约为 31,400 欧姆。回想一下，线圈导线的欧姆电阻通常为几欧姆。

从上面的公式可以看出，通过线圈的电流和线圈中的电压的变化发生在不同的相位，电流的相位总是小于电压pi/2的相位。因此，最大电流出现在最大应力出现后四分之一周期。

在感性电阻中，由于自感电动势的制动作用，电流滞后于电压90度，阻止了电流的变化（增加和减少），所以后来在带线圈的电路中观察到最大电流比最大电压。

线圈和电容联合作用

如果在交流电路中串联一个带电容的线圈，那么线圈电压会在时间上超前电容电压半个周期，即相位超前180度。

电容电阻和电感电阻分别称为 反应物…能量不像在有源电阻中那样消耗在无功电阻中。当电容器中的电场消失时，存储在电容器中的能量会周期性地返回到电源。

线圈也是如此：由于线圈的磁场是由电流产生的，其中的能量在四分之一的周期内积累，并在下一个四分之一的周期内返回到源头。在本文中，我们讨论了严格遵守这些规定的正弦交流电。

在交流正弦电路中，铁芯电感称为 令人窒息传统上用于限流。与变阻器相比，它们的优势在于能量不会以热量的形式大量耗散。