非线性电路
电路中非线性元件的用途
V 电路 可能包括无源元件, 电阻 这基本上取决于电流或应力,因此电流与电压不成正比。这些元件和它们进入的电路称为非线性元件。
非线性元件赋予电路线性电路无法实现的特性(电压或电流稳定、直流放大等)。它们是不可控的和可控的……第一个 - 双极 - 设计用于在不受控制因素影响的情况下工作(半导体热敏电阻和二极管),第二个 - 多极 - 当控制因素作用于它们(晶体管)时使用和晶闸管)。
非线性元件的电流-电压特性
非线性元件的电特性是电流-电压特性I(U) 实验得到的曲线表示电流对电压的依赖性,有时会给出一个近似的、便于计算的经验公式。
不受控的非线性元件具有单一的电流-电压特性,而受控的非线性元件具有一族这样的特性,其参数是控制因素。
线性元件具有恒定的电阻,因此它们的电流-电压特性是一条通过原点的直线(图 1,a)。
非线性的电流-电压特性具有不同的形状,分为相对于坐标轴对称和不对称(图1,b,c)。
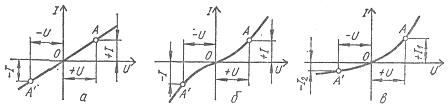
米。 1、无源元件的电流-电压特性:a——线性,b——非线性对称,c——非线性不对称
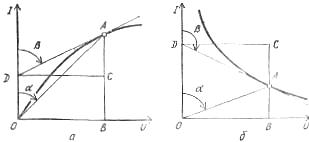
米。 2.确定电流-电压特性各段非线性元件静差电阻的曲线图:a—上升,b—下降
对于具有对称电流-电压特性的非线性元件或对于对称元件,电压方向的变化不会引起电流值的变化(图 1,b),对于具有不对称电压的非线性元件-电流特性,或对于不对称元件,具有一个相同的电压绝对值,但方向相反,电流不同(图 1,c)。因此,在直流和交流电路中使用非线性对称元件,在交流电路中通常使用非线性不平衡元件来将交流电转换为直流电。
非线性元件的特性
对于每个非线性元件,区分电流-电压特性的给定点对应的静态电阻,例如A点:
Rst = U / I = muOB / miBA = mr tgα
以及用于的微分电阻。同点A由公式确定:
Rdiff = dU / dI = muDC / miCA = mr tgβ,
其中 mi、mi、sir — 分别是电压、电流和电阻的比例。
静态电阻表征非线性元件在恒流模式下的特性,微分电阻表征电流与稳态值的小偏差。从一个点和电流-电压特性曲线到另一个点时,两者都会发生变化,第一个始终为正,第二个变量:在特性曲线的上升部分,电流-电压为正,在下降部分为负。
非线性元件的特征还在于倒数值:静态电导率 Gst 和微分电导率 G 不同或无量纲参数 —
相对电阻:
Kr = — (Rdifference /Rst)
或相对电导率:
公斤 = — (Gdifference / Gst)
线性元件的参数 Kr 和 Kilogram 都等于 1,对于非线性元件,它们与它不同,它们与 1 的差异越大,电路的非线性就越明显。
 非线性电路计算
非线性电路计算
非线性电路是基于图形和分析计算的 基尔霍夫定律 用于将交流电转换为直流电的交流电路的各个元件的伏安特性和伏安特性。
当以图形方式计算具有电流-电压特性 Iz (U1) 和 Iz (U2) 的两个串联非线性电阻器 R1 和 R2 的电路时,构建整个电路的电流-电压特性 Iz (U),其中 U = U1 + U2,其横坐标点为等纵坐标的非线性电阻电流-电压特性各点的横坐标相加得到的点(图3,a,b)。
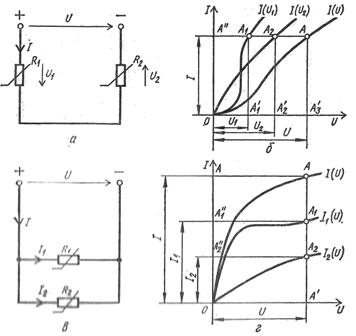
米。 3. 非线性电路图及特性:a——非线性电阻串联电路,b——单个元件和串联电路的伏安特性,c——非线性电阻并联方案,d — 单个元件和并联电路的伏安特性。
这条曲线的存在使得电压 U 可以找到电流 Az 以及电阻器端子处的电压 U1 和 U2。
同理计算两个电阻并联的电路。 R1 和 R2 具有电流-电压特性 I1 (U) 和 Az2 (U),为此构建了整个电路的电流-电压特性 Az(U),其中 Az = I1+I2,在此基础上,使用给定电压U,求电流 Az 、I1、I2(oriz. 3、c、d)。
计算非线性电路的分析方法是通过相应的数学函数方程来表示非线性元件的电压特性,从而可以得出电路所必需的状态方程。 .由于此类非线性方程的求解往往会造成很大的困难,因此当非线性元件的电流-电压特性的操作部分可以被拉直时,非线性电路的解析方法计算是很方便的。这使您可以通过线性方程来描述电路的电气状态,而不会给求解它们带来困难。
电气工程基础:

