有源无功电阻、电阻三角

活性和反应性

直流电路中通路和消费者提供的电阻称为欧姆电阻。

如果任何电线包含在交流电路中，那么它的电阻会比直流电路中的电阻略高。这是由于一种称为集肤效应的现象（表面效应).

其本质如下。当交流电流过导线时，其内部存在交变磁场，与导线交叉。该场的磁力线在导体中感应出 EMF，但是，它在导体横截面的不同点上并不相同：更多地朝向横截面的中心，而更少地朝向外围。

这是因为靠近中心的点被大量的力线交叉。在这种电动势的作用下，交流电不会均匀地分布在整个导体截面上，而是更靠近其表面。

这相当于减少了导体的有用横截面，从而增加了它对交流电的抵抗力。例如，一根长 1 公里、直径 4 毫米的铜线可抵抗：直流 — 1.86 欧姆，交流 800 赫兹 — 1.87 欧姆，交流 10,000 赫兹 — 2.90 欧姆。

导体对通过它的交流电提供的电阻称为有源电阻。

如果任何消费者不包含电感和电容（白炽灯泡，加热设备），那么它也将是一个有源交流电阻。

有功电阻——表征电路（或其面积）由于电能不可逆地转化为其他形式（主要是热）而对电流产生的电阻的物理量。以欧姆表示。

主动电阻取决于 交流频率随其增加而增加。

然而，许多消费者在交流电流过时具有电感和电容特性。这些消费者包括变压器、扼流圈、 电磁铁, 电容器，不同类型的电线和许多其他。

经过他们时 交流电 由于消费者存在电感和电容特性，因此不仅要考虑活性，还要考虑反应性。

众所周知，如果通过每个线圈的直流电被中断和关闭，那么在电流变化的同时，线圈内部的磁通量也会发生变化，从而产生自感电动势在里面。

在 AC 电路中的线圈中也会观察到相同的情况，唯一的区别是节拍的幅度和 in 和 to 都在不断变化。因此，穿过线圈的磁通量大小会不断变化而感应 自感电动势.

但是自感电动势的方向总是与电流的变化方向相反。所以，随着线圈中电流的增加，自感电动势会趋向于减缓电流的增加，而随着电流的减小，则相反，它会趋于保持消失的电流。

由此可见，交流电路中的线圈（导体）产生的自感电动势总是与电流反向作用，减缓其变化。换句话说，自感电动势可以被认为是一个附加电阻，它与线圈的有源电阻一起抵消通过线圈的交流电。

电动势通过自感对交流电提供的电阻称为感性电阻。

感应电阻会随着用户（电路）的电感越大，交流电的频率越高。该电阻由公式 xl = ωL 表示，其中 xl 是以欧姆为单位的电感电阻； L——亨利电感（gn）； ω — 角频率，其中 f — 当前频率）。

除了电感电阻外，还有电容，因为在某些情况下，电线和线圈中存在电容，并且在交流电路中包含电容器。随着用电器（电路）的电容 C 和电流角频率的增加，电容电阻减小。

电容电阻等于 xc = 1 / ωC，其中 xc — 以欧姆为单位的电容电阻，ω — 角频率，C — 以法拉为单位的用户容量。

在这里阅读更多相关信息： 电气工程中的电抗

电阻三角

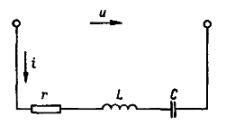
考虑一个有源元件电阻 r、电感 L 和电容 C 的电路。

米。 1、有电阻、电感、电容的交流电路。

这种电路的阻抗为 z = √r2+ (хl — xc)2) = √r2 + х2)

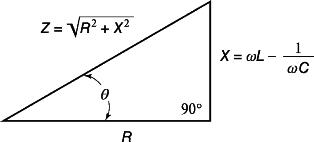
在图形上，该表达式可以用所谓的电阻三角形的形式描述。

如图。 2.电阻三角

电阻三角形的斜边代表电路的总电阻，支路 - 有源电阻和无功电阻。

如果电路的其中一个电阻（有源或无功），例如比另一个小 10 倍或更多，则较小的可以忽略不计，这很容易通过直接计算来检查。