异步电机运行

感应电机的运行以图形方式表示速度 n2、效率 η、有用转矩（轴转矩）M2、功率因数 cos φ 和定子电流 I1 在 U1 = const f1 = const 时对有用功率 P2 的依赖性。

速度特性n2=f(P2)。感应电动机的转子速度 n2 = n1 (1 — s)。

载玻片 s = Pe2 / Rem，即感应电机的滑差及其速度由转子中的电损耗与电磁功率之比决定。忽略空转时转子的电损耗，我们可以取 Pe2 = 0，因此 s ≈ 0 和 n20 ≈ n1。

随着轴负载的增加 异步引擎 比率 s = Pe2 / Pem 增加，在额定负载下达到 0.01 - 0.08 的值。因此，依赖性n2＝f(P2)是稍微向横坐标轴倾斜的曲线。然而，随着电机转子有源电阻r2'的增大，该曲线的斜率增大。在这种情况下，随着负载P2的波动，感应电动机n2的频率变化增加。这是因为当 r2 ' 增加时，转子中的电损耗增加。

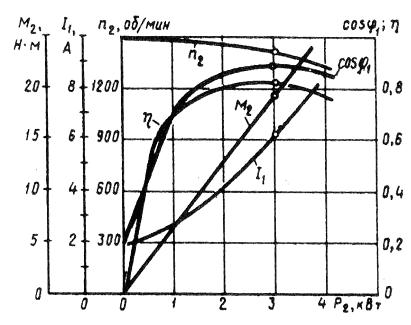
米。一、感应电动机的运行特点

依赖性 M2 = f (P2)。异步电机 M2 轴的有用扭矩对有用功率 P2 的依赖性由表达式 M2 = P2 / ω2 = 60 P2 / (2πn2) = 9.55P2 / n2 确定，

式中 P2——有用功率，W； ω2 = 2πf 2/60 是转子的旋转角频率。

从这个表达式可以得出，如果 n2 = const，则图形 M2 = f2 (P2) 是一条直线。但是在负载 P2 增加的感应电动机中，转子的速度降低，因此轴 M2 的有用力矩随着负载的增加增加得比负载快一点，因此图 M2 = f (P2 ) 具有曲线形状。

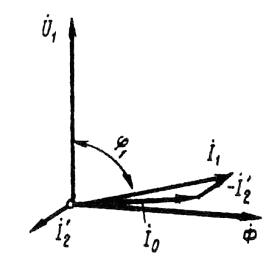米。 2. 低负载感应电动机矢量图

依赖性 cos φ1 = f (P2)。由于感应电机的定子电流 I1 具有在定子中产生磁场所必需的无功（感性）分量，因此感应电机的功率因数小于 1。功率因数的最低值对应于空转。这是因为电动机的无功电流 I0 在任何负载下几乎保持不变。因此，在低电机负载下，定子电流较小且无功（I1 ≈ I0）。因此，定子电流相对于电压的相移很大 (φ1 ≈ φ0)，仅略小于 90°（图 2）。

感应电动机的空载功率因数通常小于0.2。随着电机轴上负载的增加，电流 I1 的有功分量增加，功率因数增加，在接近标称负载时达到最高值 (0.80 — 0.90)。电机轴上负载的进一步增加伴随着 cos φ1 的减小，这可以解释为由于转差增加导致转子的感应电阻 (x2s) 增加，因此频率增加转子中的电流。

为了提高感应电机的功率因数，电机始终或至少大部分时间以接近额定负载的负载运行是极其重要的。这只能通过正确选择发动机功率来实现。如果电机在大部分时间都在负载下运行，那么要增加 cos φ1，建议降低提供给电机的电压 U1。例如，在定子绕组为三角形连接的电机中，这可以通过重新连接星形定子绕组来实现，这将导致相电压降低一个系数。在这种情况下，定子磁通量以及励磁电流都会降低大约一个因子。此外，定子电流的有功分量略有增加。所有这些都有助于提高发动机的功率因数。

在图。图 3 显示了当定子绕组以星形（曲线 1）和三角形（曲线 2）连接时，异步电动机 cos φ1 对负载的依赖关系图。

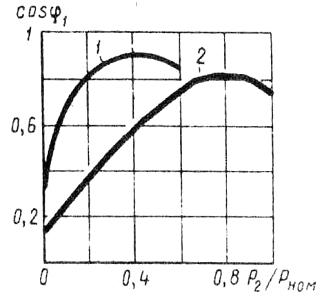
米。 3. 电机定子绕组采用星形（1）和三角形（2）连接时，cos φ1 对负载的依赖性