连续振荡和参数共振

连续振动——能量不随时间变化的振动。在真实的物理系统中，总会有一些原因导致振动能向热能的转变（例如机械系统中的摩擦，电气系统中的主动电阻）。

因此，只有补充这些能量损失才能获得无阻尼振荡。由于来自外部源的能量，这种补充在自振荡系统中自动发生。连续电磁振荡的应用极其广泛。使用不同的生成器来获取它们。

为了使（摆动圆或摆的）电气或机械振动不受阻尼，必须始终补偿阻力或摩擦损失。

例如，您可以使用交变 EMF 作用于振荡电路，这将周期性地增加线圈中的电流，并相应地保持电容器中的电压幅度。或者您可以用类似的方式推动钟摆，使其保持和谐摆动。

大家知道，振荡电路线圈的磁场能量的大小与其电感量和电流有如下关系（第二式为电容器电场的能量 相同的轮廓轮廓）

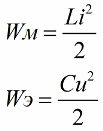
从第一个公式可以清楚地看出，如果我们周期性地增加线圈中的电流，作用于交变 EMF 电路，那么（通过增加或减少公式中的第二个因素——电流）我们将周期性地为该电路补充能量。

严格按电路的自然自由振荡时间，即在谐振频率作用于电路，我们会得到电谐振现象，因为它在谐振频率 振荡系统 最集中地吸收提供给它的能量。

但是，如果您不定期更改第二个因素（不是电流或电压），而是第一个因素 - 电感或电容，会怎样？在这种情况下，电路的能量也会发生变化。

例如，定期将磁芯推入和推出线圈或推入和推出电容器电介质, — 我们还得到电路中能量的非常明确的周期性变化。

我们为线圈电感的单位变化写下这个位置：

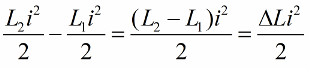
电路摆动的最显着影响是及时改变电感。例如，如果我们在任何时刻采用相同的电路，当一些电流 i 已经流过它时，将一个磁芯引入线圈，那么能量将改变如下：

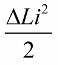
现在让电路本身出现自由振荡，但是在经过四分之一周期后能量完全传递到电容器并且线圈中的电流变为零的那一刻，我们将突然从线圈中取出磁芯电感将恢复到其原始状态，即初始值 L。当磁芯被移除时，不需要对磁场做任何功。因此，当铁芯被推入线圈时，电路接收到能量，因为我们工作了，其值：

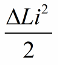
四分之一周期后，电容开始放电，其能量再次转化为线圈磁场的能量，当磁场达到一定幅度时，我们将再次对铁芯进行猛烈的挤压。电感再次增加，增加了相同的量。

同样，在零电流下，我们将电感返回到其原始值。这样一来，如果每半个周期的能量增益超过电阻损耗，则环路的能量会一直增加，振荡幅度也会增加。这种情况由不等式表示：

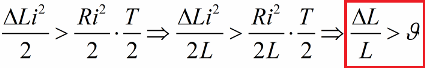
在这里，我们将这个不等式的两边除以 L，并写下了对数递减的特定值通过跳跃进行参数激励的可能性的条件。

建议每个周期更改电感（或电容）两次，因此参数更改的频率（参数谐振频率）应为振荡系统固有频率的两倍：

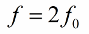
于是电路中的振荡激励路径就出现了，无需直接改变电动势或电流。电路中的初始波动电流总是以这种或那种方式存在，这甚至没有考虑大气中射频振荡的干扰。

如果电感（或电容）没有跳跃变化，而是谐波变化，那么振荡发生的条件看起来会有点不同：

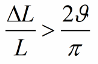
由于电容和电感是电路参数（如钟摆的质量或弹簧的弹性），因此激发振荡的方法也称为参数激励。

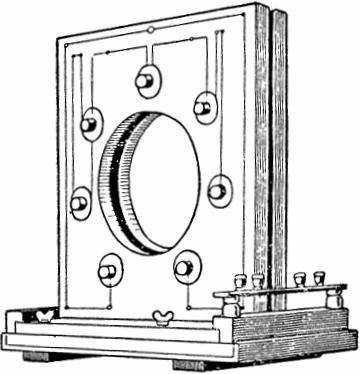
这一现象在20世纪初被苏联物理学家曼德尔施塔姆和帕帕列西发现并进行了实践研究。基于这一物理现象，他们建造了第一台功率为4千瓦、可变电感的参量交流发电机。

在发电机的设计中，七对扁平线圈位于框架的两侧，在其空腔中有一个带有突起的铁磁性圆盘旋转。当圆盘被电机驱动旋转时，其突起周期性地进出每对线圈之间的空间，从而改变电感并激发振荡。