电毛细管现象

如果电解质表面带电，则其表面的表面张力不仅取决于相邻相的化学成分，还取决于它们的电性能。这些特性是表面电荷密度和界面处的电势差。

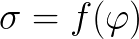
这种现象的表面张力对电位差的依赖性 (e) 由电毛细管曲线描述。观察到这种依赖性的表面现象称为电毛细管现象。

允许电极电势在电极-电解质界面处以某种方式发生变化。在这种情况下，金属表面有离子形成表面电荷并导致双电层的存在，尽管这里根本没有外部电动势。

同电荷离子在界面表面相互排斥，从而补偿液体分子的收缩力。结果，表面张力变得比在电极上没有过量电势的情况下低。

如果向电极施加相反符号的电荷，则表面张力将增加，因为离子的相互排斥力将减小。

在排斥离子的静电力对吸引力进行绝对补偿的情况下，表面张力达到最大值。如果我们继续提供电荷，那么随着新的表面电荷的产生和增长，表面张力会降低。

在某些情况下，电毛细现象的重要性非常大。它们可以改变液体和固体的表面张力，以及影响粘附、润湿和分散等胶体化学过程。

让我们再次将注意力转向这种依赖的定性方面。在热力学上，表面张力被定义为形成单位表面的等温过程的功。

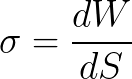
当表面上存在同名电荷时，它们会相互静电排斥。静电排斥力将切向地指向表面，无论如何都会试图增加它的面积。因此，拉伸带电表面所需的功将小于拉伸类似但电中性表面所需的功。

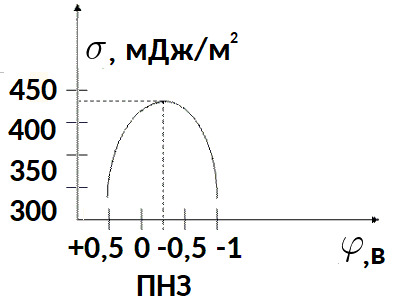
例如，让我们以室温下电解质水溶液中汞的电毛细管曲线为例。

在最大表面张力点电荷为零。在这些条件下，汞表面呈电中性。因此，电极表面张力最大时的电位是零电荷电位（ZCP）。

零电荷电势的大小与液体电解质的性质和溶液的化学成分有关。电毛细管曲线的左侧，表面电势小于零电荷电势，称为阳极支路。右侧是阴极支路。

应该注意的是，非常小的电势变化（大约 0.1 V）会导致表面张力发生显着变化（大约每平方米 10 mJ）。

表面张力对电势的依赖性由李普曼方程描述：

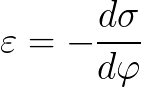
电毛细管现象在金属上的各种涂层应用中找到了实际应用——它们使调节固体金属与液体的润湿成为可能。李普曼方程允许计算双电层的表面电荷和电容。

借助电毛细管现象，可以确定表面活性剂的表面活性，因为它们的离子具有特定的吸附。在熔融金属（锌、铝、镉、镓）中，确定了它们的吸附能力。

电毛细管理论解释了极谱法中的最大值。电极的润湿性、硬度和摩擦系数对其电位的依赖性也指电毛细管现象。