电动机的加热和冷却

正确确定各种金属切削机床、机构和机器的电动机功率非常重要。如果动力不足，就不可能充分利用机器的生产能力来执行计划的工艺流程。如果功率不足，电动机会过早失效。

高估电动机的功率会导致系统充电不足，从而导致电动机使用不充分、运行效率低和功率因数小（对于异步电动机）。此外，当发动机功率被高估时，资本和运营成本会增加。

操作机器所需的功率，以及因此由电动机产生的功率，在机器操作期间发生变化。电动机上的负载可以通过负载图（图 1）来表征，它是电机轴的功率、扭矩或电流对时间的依赖性。工件加工完成后，停机，测量工件，更换工件。然后再次重复加载计划（当处理相同类型的零件时）。

为确保在这种可变负载下正常运行，电动机必须在加工过程中产生所需的最高功率，并且根据此负载计划在连续运行期间不会过热。电动机的允许过载由其电气特性决定。

米。 1.加工同类零件时加载进度表

当发动机运转时， 能量（和功率）损失导致它升温。电动机消耗的部分能量用于加热其绕组，用于加热电机的磁路 迟滞 和涡流携带摩擦和空气摩擦。绕组的热损耗与电流的平方成正比，称为变量 (ΔРtrans)... 电机中的剩余损耗在一定程度上取决于其负载，通常称为常数 (ΔРpos)。

电动机的允许发热由其结构中最不耐热的材料决定。这种材料是其线圈的绝缘层。

以下用于绝缘电机：

• 棉和丝绸织物、纱线、纸张和未浸渍绝缘化合物的有机纤维材料（耐热等级U）；

• 相同的材料，浸渍（A 类）；

• 合成有机薄膜（E 类）；

• 石棉、云母、玻璃纤维和有机粘合剂制成的材料（B 类）；

• 相同，但使用合成粘合剂和浸渍剂（F 类）；

• 相同的材料，但含有硅粘合剂和浸渍剂（H 类）；

• 不含粘合剂或含有无机粘合剂的云母、陶瓷、玻璃、石英（C 类）。

绝缘等级U、A、E、B、F、H分别允许最高温度90、105、120、130、155、180℃。C级的极限温度超过180℃，受绝缘材料性能限制用料。

电动机负载相同，在不同的环境温度下，其发热会不均匀。环境的设计温度t0为40°C。在这个温度下，电动机的标称功率值被确定。电动机的温度升高超过环境温度称为过热：

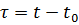
合成绝缘材料的使用正在扩大。特别是，硅绝缘材料可确保电机在热带条件下运行时的高可靠性。

发动机不同部位产生的热量不同程度地影响绝缘体的加热。此外，热交换发生在电动机的各个部件之间，其性质根据负载条件而变化。

电动机各个部件的不同加热以及它们之间的热传递使过程的分析研究复杂化。因此，为简单起见，有条件地假设电动机是热均匀且无限导热的物体。一般认为，电动机释放到环境中的热量与过热度成正比。在这种情况下，热辐射可以忽略不计，因为电机的绝对加热温度很低。在给定的假设下考虑电动机的加热过程。

电动机工作时，在时间dt内放出热量dq。该热量 dq1 的一部分被电动机的质量吸收，结果电动机的温度 t 和过热 τ 增加。剩余的热量 dq2 从发动机释放到环境中。因此等式可以写成

随着发动机温度升高，热量 dq2 增加。在一定的过热值下，电动机释放的热量将与环境中释放的热量一样多；则 dq = dq2 和 dq1 = 0。电动机的温度停止升高，过热达到稳定值 τу。

在上述假设下，方程可以写成如下形式：

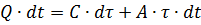
其中 Q 是由于电动机损耗引起的热功率，J / s； A——来自发动机的传热，即发动机与环境温差1oC时，单位时间内发动机释放到环境中的热量，J/s-deg； C是电机的热容量，即使发动机温度升高 1°C 所需的热量，J/deg。

分离方程中的变量，我们有

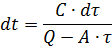
我们在从零到某个时间 t 的当前值的范围内对等式左侧进行积分，在从电动机的初始过热 τ0 到当前过热值 τ 的范围内对等式右侧进行积分：

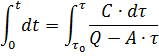
求解 τ 的方程式，我们得到用于加热电动机的方程式：

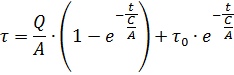
让我们表示 C / A = T 并确定该比率的维度：

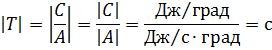
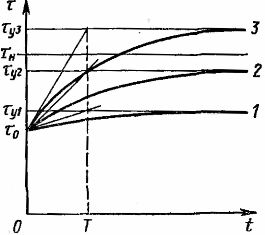
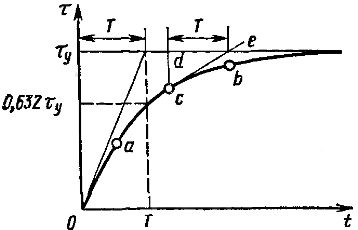
米。 2. 表征电动机发热的曲线

米。 3、加热时间常数的确定

称为量T，它具有电动机加热时间常数的时间量纲。根据这个符号，加热方程可以改写为

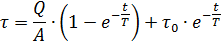
从等式中可以看出，当我们得到 — 稳态过热值。

当电动机上的负载发生变化时，损耗量会发生变化，因此 Q 值也会发生变化。这会导致 τу 值发生变化。

在图。图 2 显示了对应于不同负载值的最后一个方程的加热曲线 1、2、3。当 τу 超过允许的过热值 τn 时，电动机的连续运行是不可接受的。从等式和图表（图 2）可以看出，过热度的增加是渐近的。

当我们将值 t = 3T 代入等式时，我们得到的 τ 值大约仅比 τy 小 5%。因此，在时间 t = 3T 期间，实际上可以认为加热过程已完成。

如果在加热曲线的任意点（图 3）绘制加热曲线的切线，然后通过同一点绘制垂直线，然后在刻度上在切线和垂直线之间闭合的渐近线段 de横坐标轴的等于T。如果我们在方程中取Q = 0，我们得到电机冷却方程：

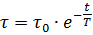
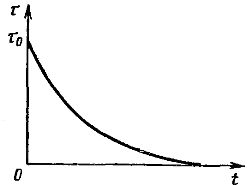
冷却曲线如图 1 所示。 4，对应于这个等式。

加热的时间常数取决于电动机的大小及其对环境影响的保护形式。对于打开和保护的小功率电动机，加热时间为 20-30 分钟。对于封闭式大功率电动机，达到2-3小时。

如上所述，所陈述的电动机加热理论是近似的并且基于粗略的假设。因此，实验测量的加热曲线与理论曲线有很大差异。如果，对于实验加热曲线的不同点，如图所示的结构。 3、事实证明T的值随着时间的增加而增加。因此，根据该等式进行的所有计算都应视为近似值。在这些计算中，建议使用以图形方式确定的常数 T 作为加热曲线的起点。这个 T 值是最小的，并且在使用时提供一定的发动机功率余量。

米。 4.发动机冷却曲线

实验测量的冷却曲线与理论曲线的差异甚至超过加热曲线。由于在没有通风的情况下热传递减少，对应于发动机关闭的冷却时间常数明显长于加热时间常数。