并励电机制动方式

并励电机制动方式电驱动中的发动机制动方式与发动机一起使用。电动机作为电制动器在实践中广泛用于缩短停车和换向时间、降低转速、防止行驶速度过快等多种情况。

电动机作为电制动器的操作基于电机的可逆性原理，即电动机在特定条件下切换到发电机模式。

在实践中，三种模式用于制动：

1) 能量返回电网的发电机（再生），

2）电动，

3）反对。

在直角坐标系中构建机械特性时，重要的是确定电机和制动模式下电机扭矩和转速的符号。为此，通常以电机模式为主，将电机在该模式下的转速和转矩视为正值。在这方面，电机模式的特性 n = f (M) 位于第一象限（图 1）。机械特性在制动模式中的位置取决于扭矩和转速的符号。

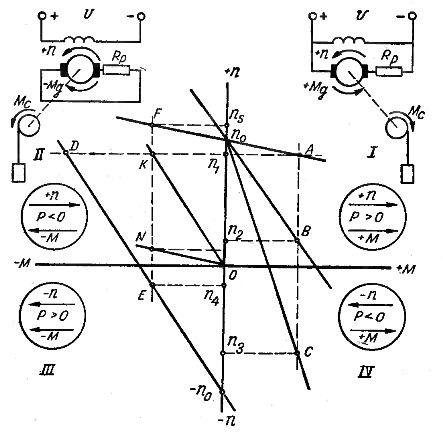
并励电机在电机和制动模式下的接线图和机械特性

米。 1…并联励磁电机在电机和制动模式下的连接图和机械特性。

让我们考虑这些模式和并励电机机械特性的相应部分。

反对。

电驱动器的状态由电机扭矩 Md 和静态负载扭矩 Mc 的共同作用决定。例如，用绞车提升负载时的稳态转速n1，当Md = Ms时，它对应于发动机以自然特性（图1点A）运行。如果在电机的电枢回路中引入了额外的电阻，则转速会因过渡到变阻器特性而降低（B点对应速度n2，Md = Ms）。

电机电枢电路中附加电阻的进一步逐渐增加（例如，增加到对应于 n0Characteristics C 部分的值）将首先导致负载提升停止，然后导致旋转方向发生变化，即负载会下降（C点）。这样的政权被称为反对派。

直流电机

相反模式下，时刻Md 为正号。转速的符号变为负值。因此，对立模式的力学特征在第四象限，模式本身是生成的。这是根据用于确定扭矩和转速符号的公认条件得出的。

事实上，机械功率与 n 和 M 的乘积成正比，在电机模式下它具有正号并且从电机指向工作机器。在反向模式下，由于n的负号和M的正号，它们的乘积将为负，因此，机械功率以相反的方向传递——从工作机到电动机（发电机模式）。在图。电机和制动模式中的 1 个字符 n 和 M 以圆圈和箭头显示。

对立模态对应的机械特性段是电机模态特性从第一象限到第四象限的自然延伸。

从将引擎切换到相反模式的考虑示例中，可以看出 e。 ETC。 c. 电机根据旋转速度，与最后一个电机同时，在越过零值时，改变符号并根据电源电压动作：U = (-Д) +II amRfrom where I我是我是 = (U + E) / R

为了限制电流，在电机的电枢电路中包含一个很大的电阻，通常等于启动电阻的两倍。对冲模式的特点是轴侧的机械能和电网的电能被提供给电机，而这一切都用于加热电枢：Pm+Re = EI + UI = Аз2(Ри + AZ 分机）

相反的模式也可以通过在相反的旋转方向上切换绕组来获得，而电枢由于动能的储备而继续在相同的方向上旋转（例如，当具有反应静力矩的机器 - 风扇停止）。

根据电机模式读取符号n和M的可接受条件，将电机切换到反转时，坐标轴的正方向应该改变，即电机模式现在在第三象限，和反对派 - 在第二个。

因此，如果电机在 A 点以电机模式运行，则在切换的瞬间，当速度尚未改变时，它将具有新的特性，在 D 点的第二象限。停止将发生在点特性 DE (-n0)，如果发动机在速度 t = 0 时没有关闭，它将在 E 点根据该特性工作，以相反的方向以速度 -n4 旋转机器（风扇）。

电动制动方式

通过将电机电枢与网络断开并将其连接到单独的外部电阻来实现电动制动（图 1，第二象限）。显然，这种模式与独立励磁直流发电机的运行差别不大。在自然特性（直接 n0）上工作对应于短路模式，由于电流大，在这种情况下制动只能在低速时进行。

在电动制动模式下，电枢与U网络断开，因此：U = 0； ω0 = U / c = 0

机械特性方程的形式为：ω = (-RM) / c2 或 ω = (-Ri + Rext / 9.55se2) M

电动力制动的机械特性是通源的，即随着车速的降低，发动机制动力矩减小。

特性曲线的斜率与电机模式相同，由电枢电路中的电阻值决定。电动制动比相反的更经济，因为电机从网络消耗的能量仅用于励磁。

电枢电流的大小以及制动转矩取决于旋转速度和电枢电路的电阻：I = -E/ R = -sω /R

能量返回电网的发电机模式

只有当静态扭矩的作用方向与电机扭矩一致时，才可以使用此模式。在两个力矩（发动机扭矩和工作机器扭矩）的影响下，驱动器的转速和 e。 ETC。 c. 电机开始上升，电机电流和转矩减小： I = (U — E)/R= (U — сω)/R

当 U = E、I = 0 和 n = n0 时，速度的进一步增加首先导致理想怠速模式，然后是 e 等。 c. 电机将变得超过施加的电压，电机将进入发电机模式，即开始向网络提供能量。

该模式下的机械特性是电机模式特性的自然延伸，位于第二象限。转速的方向没有改变，依旧是正值，力矩是负号。在能量返回网络的发电机模式的机械特性方程中，力矩的符号会发生变化，因此将具有以下形式：ω = ωo + (R / c2) M. 或 ω = ωo + (R /9.55 ° Cd3) M。

在实践中，再生制动模式仅在具有潜在静态力矩的高速驱动器中使用，例如在高速降低负载时。