单相变压器的工作原理和装置
单相空载变压器
电气工程中的变压器被称为这样的电气设备,其中来自一个固定线圈的交流电能被传输到另一个未与第一个线圈电连接的固定线圈。
将能量从一个线圈传输到另一个的链接是磁通量,它与两个线圈互锁,并且在大小和方向上不断变化。
米。 1.
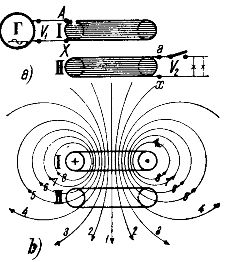
在图。图 1a 显示了由两个绕组 / 和 / / 组成的最简单的变压器,一个在另一个上面同轴排列。到卷/交付 交流电 来自交流发电机 D。该绕组称为初级绕组或初级绕组。绕组 // 称为次级绕组或次级绕组,电路通过电能接收器连接。

变压器的工作原理
变压器的动作如下。当电流在初级绕组中流动时/它被创建 磁场,其力线不仅渗透到产生它们的绕组中,而且还部分渗透到次级绕组中 //。初级绕组产生的力线分布的近似图如图 1 所示。 1b.
从图中可以看出,所有的力线都是围绕线圈/的导体闭合的,但在图在图 1b 中,电线 1、2、3、4 也闭合在线圈 // 的电线周围。因此线圈//通过磁力线磁耦合到线圈/。
线圈/和//同轴布置的磁耦合程度取决于它们之间的距离:线圈彼此距离越远,它们之间的磁耦合越小,因为作用在线圈上的力线越少线圈/粘在线圈上//。
由于线圈 / 通过,正如我们假设的那样, 单相交流电,也就是电流随着时间的推移按照某种规律变化,比如按照正弦规律,那么它产生的磁场也会按照同样的规律随时间变化。
例如,当线圈中的电流/通过最大值时,则其产生的磁通量也通过最大值;当线圈中的电流/通过零时,方向改变,则磁通量也通过零,方向也改变。
由于改变线圈 / 中的电流,线圈 / 和 // 都被磁通量穿透,不断改变其值和方向。根据电磁感应的基本定律,穿过线圈的磁通量每发生变化,线圈中就会感应出交流电 电动势……在我们的例子中,自感电动势是在线圈/中感应出来的,而互感电动势是在线圈//中感应出来的。
如果线圈的末端 // 连接到电能接收器电路(见图 1a),则该电路中将出现电流;因此接收器将接收电力。同时,能量将被引导至绕组/从发电机,几乎等于绕组//提供给电路的能量。这样,来自一个线圈的电能将传输到第二个线圈的电路,第二个线圈与第一个线圈在电流(金属)上完全无关,在这种情况下,能量传输的方式只是交变磁通量。
如图所示1a,变压器非常不完善,因为初级绕组/和次级绕组//之间几乎没有磁耦合。
一般而言,两个线圈的磁耦合是通过耦合到两个线圈的磁通量与一个线圈产生的磁通量之比来估计的。
如图。从图1b可以看出,只有线圈/的部分磁力线在线圈//周围闭合。电源线的另一部分(在图 1b 中——线 6、7、8)仅在线圈 / 周围闭合。这些电源线根本不参与从第一个线圈到第二个线圈的电能传输,它们形成所谓的杂散场。
为了增加初级和次级绕组之间的磁耦合,同时降低磁通通过的磁阻,技术变压器的绕组放置在完全封闭的铁芯上。
图 1 示意性地显示了变压器实施的第一个示例。 2 所谓棒式单相变压器。其初级、次级线圈c1、c2装在铁棒a—a上,两端接有铁板b—b,称为磁轭。这样,两个杆a、a和两个磁轭b、b形成一个闭合的铁环,其中通过被初级和次级绕组阻挡的磁通量。这个铁环就叫做变压器的铁芯。
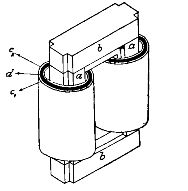 米。 2.
米。 2.
变压器的第二个实施例示意性地显示在图1中。 3 所谓的铠装型单相变压器。在这个变压器中,初级和次级绕组 c,每个都由一排扁平绕组组成,放置在由两个铁环 a 和 b 的两根杆形成的铁芯上。围绕绕组的环 a 和 b 几乎完全覆盖有铠装,因此所描述的变压器称为铠装变压器。通过线圈 c 内部的磁通量被分成相等的两部分,每一部分都被封闭在自己的铁环中。
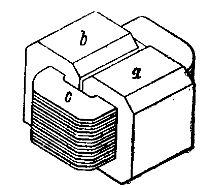
米。 3个
在变压器中使用闭合铁磁路可显着降低泄漏电流。在这种变压器中,连接到初级和次级绕组的磁通几乎彼此相等。如果我们假设初级和次级绕组被相同的磁通量穿透,我们可以根据绕组电动势的瞬时值的总感应冲击写出表达式:
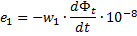
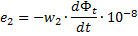
在这些表达式中,w1和w2——初级和次级绕组的匝数,dFt是每个时间元dt的磁通量在穿透绕组中的变化量,因此存在磁通量变化率.从最后的表达式,可以得到以下关系:
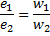
IE。在初级和次级绕组/和//中表示的瞬时电动势以与线圈匝数相同的方式相互关联。最后的结论不仅对电动势的瞬时值有效,而且对它们的最大有效值也有效。
初级绕组中感应出的电动势,作为自感电动势,几乎完全平衡施加在同一绕组上的电压...如果E1和U1你表示电动势的有效值 \u200b\u200b初级绕组和施加在它上面的电压,那么你可以写:
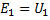
在所考虑的情况下,次级绕组中感应的电动势等于该绕组两端的电压。
如果像上一个一样,通过E2和U2表示次级绕组的电动势有效值和两端电压,那么你可以写:
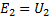
因此,通过在变压器的一个绕组上施加一些电压,您可以在另一个线圈的两端获得任何电压,您只需要在这些线圈的匝数之间取一个合适的比率即可。这就是变压器的主要特性。
初级绕组匝数与次级绕组匝数之比称为 变压器变压比... 我们将表示变换系数 kT。
因此,可以这样写:
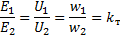
变比小于1的变压器称为升压变压器,因为次级绕组的电压,或所谓的次级电压,大于初级绕组的电压,或所谓的初级电压.变比大于1的变压器称为降压变压器,因为它的次级电压小于初级。

单相变压器带载运行
在变压器空转期间,磁通量由初级绕组电流或初级绕组的磁动势产生。由于变压器的磁路由铁制成,因此磁阻小,一般假定初级绕组的匝数较大,变压器的空载电流较小,为5-正常值的 10%。
如果把次级线圈接上某个电阻,那么随着次级线圈中电流的出现,这个线圈的磁动势也会出现。
根据楞次定律,次级线圈的磁动势与初级线圈的磁动势相反
看起来这种情况下的磁通量应该会减少,但如果在初级绕组上施加恒定电压,那么磁通量几乎不会减少。
实际上,变压器带载时在初级绕组中感应的电动势几乎等于外加电压。该电动势与磁通量成正比。因此,如果初级电压大小恒定,则负载下的电动势应与变压器空载运行期间的电动势几乎相同。这种情况导致磁通量在任何负载下几乎完全恒定。
 因此,在原边电压一定的情况下,变压器的磁通量几乎不随负载的变化而变化,可以假定与空载运行时的磁通量相等。
因此,在原边电压一定的情况下,变压器的磁通量几乎不随负载的变化而变化,可以假定与空载运行时的磁通量相等。
变压器的磁通量之所以能够在负载下保持其值,只是因为当次级绕组中出现电流时,初级绕组中的电流也增加,以至于初级和次级的磁动势或安匝数之间存在差异绕组在空转期间保持几乎等于磁动势或安匝数……因此,次级绕组中退磁磁动势或安匝数的出现伴随着初级绕组磁动势的自动增加。
如上所述,由于产生变压器磁通需要较小的磁动势,因此可以说次级磁动势的增加伴随着初级磁动势的增加,其大小几乎相同。
因此,可以这样写:
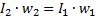
从这个等式可以得到变压器的第二个主要特性,即比率:
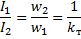
其中 kt 是转换因子。
因此,变压器初级和次级绕组的电流之比等于1除以变压比。
所以, 变压器的主要特性 有关系
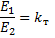
和
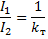
如果我们将关系的左侧相乘,右侧相乘,我们得到
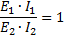
和
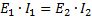
最后一个等式给出了变压器的第三个特性,可以用这样的话来表示:变压器次级绕组传递的功率(以伏安表示)几乎等于传递给初级绕组的功率(以伏安表示) .
如果我们忽略绕组铜和变压器铁芯中的能量损失,那么我们可以说从电源提供给变压器初级绕组的所有功率都转移到了它的次级绕组,并且发射机是磁通量。
