感应电动机在不同模式、电压和频率下的机械特性
感应电动机的机械特性可以表示为n=f(M)或n=e(I)。然而，异步电动机的机械特性通常以依赖关系的形式表示 M = f(S)，其中 C — 滑动，S = (nc-n) / nc，其中 ns — 同步速度。
在实践中，一个称为 Kloss 公式的简化公式用于机械特性的图形构造：
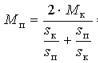
此处：Mk — 临界（最大）扭矩值。这个力矩值对应于临界滑移
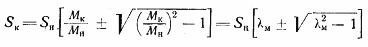
其中λm = Mk / Mn
Kloss 公式用于解决与使用感应电机执行的电力驱动相关的问题。使用 Kloss 公式，您可以根据感应电机的护照数据构建机械特性图。在实际计算中，确定根前的临界力矩时，公式中只需考虑加号即可。
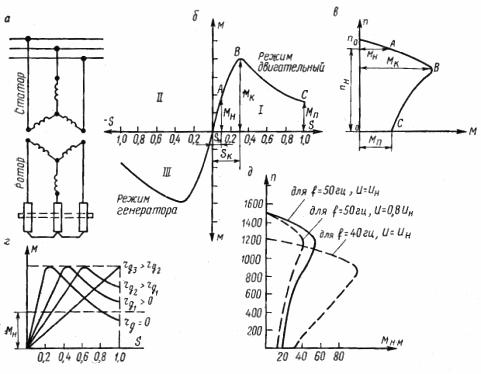
米。 1.异步电动机：a——示意图，b——机械特性 M=f(S)——电动机和发电机模式下的自然机械特性，c——电动机模式下的自然机械特性n=f(M)，d——人工变阻器的机械特性， e——不同电压和频率下的机械特性。
鼠笼式感应电动机
从图中可以看出。图 1，位于 I 和 III 象限的感应电动机的机械特性。 I 象限中的曲线部分对应于正转差值并表征异步电动机的运行模式，而在 III 象限中则表征发电机模式。发动机模式具有最大的实际意义。
电机模式的机械特性图包含三个特征点：A、B、C，并且可以有条件地分为两部分：OB 和 BC（图 1，c）。
A点对应电机的额定转矩，由公式Mn = 9.55•103•(Strn /nn)确定
这一刻对应 标称滑移，对于具有一般工业应用的发动机，其值在 1 至 7% 的范围内，即 Sn = 1 — 7%。同时，小型发动机打滑较多，大型发动机打滑较少。
用于冲击负载的高转差电机具有 Сn~15%。这些包括，例如，单串联交流电机。
特性曲线的 C 点对应于启动时电机轴上出现的初始扭矩值。这个时刻 Mp 被称为初始或开始。在这种情况下，滑移等于 1，速度为零。 启动扭矩 从参考表的数据很容易确定，该表显示了启动扭矩与标称 Mp / Mn 的比率。
在电压和电流频率恒定值下启动转矩的大小取决于转子电路中的有源电阻。在这种情况下，最初随着有源电阻的增加，启动转矩的值增加，当转子电路的有源电阻等于电动机的总感应电阻时达到最大值。随后，随着转子有功电阻的增大，初始转矩的值减小，在极限时趋于零。
C 点（图 1，b 和 c）对应于在从 n = 0 到 n = ns 的整个旋转范围内可以开发发动机的最大力矩......这个力矩称为临界（或倾覆）力矩 Mk .临界力矩也对应于临界滑移Sk。临界滑移 Sk 的值越小，标称滑移 Сn 的值越小，机械特性的刚度就越大。
起始时刻和关键时刻由标称时刻决定。根据鼠笼式电机的 GOST，必须满足条件 Mn / Mn = 0.9 — 1.2，Mk / Mn = 1.65 — 2.5。
需要注意的是，临界力矩的取值与转子回路的有源电阻无关，而临界转差Сk与该电阻成正比。这意味着随着转子电路的有效电阻的增加，临界力矩的值保持不变，但扭矩曲线的最大值向增加的转差值移动（图 1，d）。
临界转矩的大小与施加到定子上的电压的平方成正比，与定子中电压频率和电流频率的平方成反比。
例如，如果提供给电机的电压等于额定值的 85%，则临界转矩的大小将为额定电压下的 0.852 = 0.7225 = 72.25% 临界转矩。
改变频率时观察到相反的情况。例如，如果对于设计为以电流频率 = 60 Hz 运行的电机，电源电流频率 = 50 Hz，则临界力矩将大于 (60/50)2=1.44 倍其频率的官方值（图 1，e）。
临界力矩表征电机的瞬时过载能力，即表示电机能够承受多长时间（几秒内）的过载而不产生任何有害后果。
机械特性从零到最大（临界）值（见图 1，biv）的部分称为特性的稳定部分，BC 部分（图 1，c）称为不稳定部分。
这种划分可以通过以下事实来解释：在 OF 特性的增加部分，随着滑移的增加，即随着速度的降低，发动机产生的扭矩增加。这意味着随着负载的增加，即随着制动力矩的增加，电动机的转速降低，由此增加的扭矩增加。当负载减小时，反之，转速增大，转矩减小。随着负载在整个特性稳定部分的范围内变化，电机的转速和扭矩发生变化。
电机不能产生超过临界扭矩，如果制动力矩更大，电机必然会停止。正如他们所说，发动机翻车发生了。
U 和 I 恒定且转子电路中没有附加电阻的机械特性称为自然特性（具有绕线转子的鼠笼式感应电动机的特性，转子电路中没有附加电阻）。人为或变阻特性称为与转子电路中的附加电阻相对应的特性。
所有启动扭矩值都不同，取决于转子电路的有源电阻。不同大小的滑块对应相同的标称扭矩Mn。随着转子电路的电阻增加，转差增加，因此电机的速度降低。
由于转子电路中包含有源电阻，稳定部分的机械特性在增加转差的方向上被拉伸，与电阻成正比。这意味着电机速度开始根据轴负载发生显着变化，并且硬特性变得软。