电力负荷的计算
通过需求系数法确定最大负荷
这种方法最简单,归结为使用以下公式计算最大有源负载:
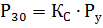
需求系数法可用于计算一般用电者、车间和企业等不同群体的负荷,该系数值有相关数据(见 计算电力负荷的系数).
在计算各组受电装置的负荷时,建议对受电装置工作在恒定负载下且占空比等于(或接近)1的组,如水泵电动机、粉丝等。
根据每组用电器得到的P30值,确定无功负荷:
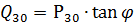
此外,tanφ 由一组给定的电力消费者的 cosφ 特性决定。
然后将有功负载和无功负载分别相加,得出总负载:
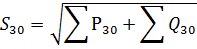
负载 ΣP30 和 ΣQ30 是各组用电器的最大值之和,而实际上必须确定最大值。因此,在确定具有大量不同组电接收器的网段的负荷时,必须引入合并最大值的系数KΣ,即
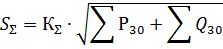
KΣ取值范围为0.8~1,计算全厂负荷时通常取其下限。
为了 独立的电子接收器 大功率,以及在设计实践中很少甚至是第一次使用的能源用户,应与技术人员一起通过明确实际负荷系数来确定需求系数。
用双表达式法确定最大载荷
这种方法是由英格提出的。 DS Livshits 最初用于确定金属加工机械单独驱动的电动机的设计负载,然后扩展到其他组的电接收器。
根据这种方法,一组具有相同操作模式的用电器的半小时最大有功负荷由以下表达式确定:
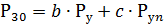
式中 Рn——最大能源用户的装机容量,b、c——同一运行模式下某一组能源用户的常数系数。
根据物理意义,计算公式的第一个成员确定平均功率,第二个成员 - 由于组中各个耗电器的最大负载重合而可能在半小时内发生的额外功率.所以:
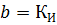
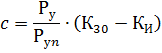
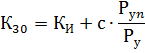
因此,对于 Pp 与 Ru 相比较小的值,这种情况发生在大量或多或少相同功率的电接收器中,K30 ≈ CP,在这种情况下可以忽略计算公式的第二项,假设 P30 ≈ bPp ≈ Psr.cm。相反,对于少量的电接收器,尤其是当它们的功率相差很大时,公式中第二项的影响就变得非常显着。
使用这种方法的计算比使用需求因子方法更麻烦。因此,双表达式方法的使用仅适用于以可变负载和低开关系数运行的能源消费者组,对于这些用户,需求系数要么根本不存在,要么可能导致错误的结果。特别地,例如,可以推荐将这种方法用于金属加工机械的电动机和周期性装载产品的小功率电阻炉。
使用此方法确定满载 S30 的方法类似于对需求因数法所描述的方法。
通过能源消费者的有效数量的方法确定最大负载。
电接收器的有效数量理解为功率相等、工作模式相同的接收器的数量,它决定了一组具有不同功率和工作模式的接收器的计算最大值的相同值。
能源消费者的有效数量由以下表达式确定:
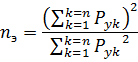
本组受电器对应的最大太阳和利用系数,根据参考表确定KM的最大系数,然后确定有功负荷的半小时最大值
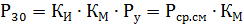
为了计算每组工作模式相同的受电设备的负荷,只有当该组内的受电设备功率差异较大时,PE的确定才有意义。
具有相同功率的 p 个电接收器包含在组中
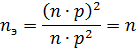
IE。电动机的有效数量等于实际数量。因此,在组内用电设备容量相同或略有不同的情况下,建议根据实际用电设备数量确定CM。
在计算多组受电器的负荷时,需要利用以下公式确定利用率的平均值:
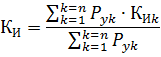
受电器有效数法适用于任何一组受电器,包括间歇工作的受电器。在后一种情况下,装机功率 Ru 降低到占空比 = 100%,即到连续运行。
有效用户数方法优于其他方法,因为作为用户数函数的最大因子参与确定负载。换句话说,此方法计算各个组的载荷总和的最大值,而不是最大值的总和,例如搜索系数法就是这种情况。
要根据 P30 的发现值计算负载 Q30 的无功分量,需要确定 tanφ。为此,有必要计算每组用电器的平均负载并根据比率确定 tanφ:
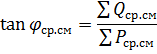
回到 PE 的定义,应该注意的是,由于有大量的组和组中各个电接收器的不同容量,发现 ΣPy2 实际上是不可接受的。因此,采用简化的方法根据电接收器的情感数量pe = ne / n的相对值来确定pe。
这个数字是从参考表中找到的,具体取决于比率:
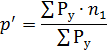
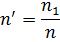
其中 n1 是受电装置的数量,每个受电装置的容量至少是最强大受电装置功率的一半,ΣPupg1 是这些受电装置的装机功率之和,n——所有用电器的数量, ΣPу——所有用电器的装机功率之和。
根据单位生产用电量的特定规范确定最大负荷
了解接收方企业、车间或技术组的计划生产率信息,并为 单位产量活性能量比,您可以使用表达式计算最大半小时活动负载,
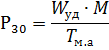
其中 Wyd 是每吨产品的比能耗,ME 是年产量,Tm.a——最大有效负荷下的年使用小时数。
在这种情况下,满载是根据加权平均年功率因数确定的:
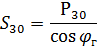
这种计算方法可以粗略地确定整个企业或生产成品的个别车间的负荷。要计算电网各个部分的负载,通常无法使用这种方法。
确定能源消耗者数量最多为五个的最大负载的具体案例
可以通过以下简化的方式计算具有少量能源消费者的组的负荷。
1、若组内有两个或三个受电器,则可将受电器的额定功率之和作为计算的最大负载:
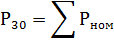
因此
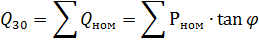
对于类型、功率和操作模式相同的电接收器,总功率的算术相加是允许的。然后,
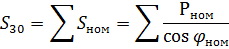
2.如果组内有4个或5个相同型号、功率、工作模式的受电装置,可根据平均负荷率计算最大负荷,此时可假设总功率的算术和成为:
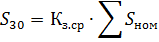
3、相同数量不同型号的受电器,计算出的最大负载必须取受电器额定功率与受电器负载系数特性的乘积之和:
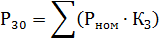
因此:
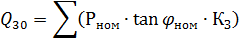
在一组存在的情况下确定最大负载,包括三相和单相电力消费者
如果固定式和移动式单相受电装置的总装机功率不超过三相受电装置总功率的15%,那么无论分布的均匀程度如何,整个负荷都可以认为是三相的单相负载的阶段。
否则,即如果单相用电设备的装机总功率超过三相受电设备总功率的15%,则单相负荷的分相分配必须按照最大实现了均匀度。
当这成功时,可以用通常的方式进行负载计数,但如果没有,则必须对负载最大的阶段进行计数。在这种情况下,可能有两种情况:
1.所有单相用电器都连接到相电压,
2.单相电接收器中也有接市电的。
在第一种情况下,对于装机功率,其实际功率的三分之一必须用于三相受电器组(如果有),用于单相受电器组 - 连接到最大负载相的功率。
根据这样得到的相功率,分别计算出各路负荷最大的相的最大负荷,再乘以3,就确定了三相线路的负荷。
在第二种情况下,负载最大的相位只能通过计算连接到网络电压的单相负载必须带到相应相位的平均功率来确定。
简化为 a 相,连接在 ab 相和 ac 相之间的单相接收器的有功功率由以下表达式确定:
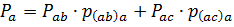
因此,此类接收器的无功功率
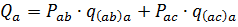
此处Рab、Ras分别为ab相与ac相间接入线电压的功率,p(ab)a、p(ac)a、q(ab)a、q(ac)a,为带电系数连接到线路电压的负载到 A 相。
通过循环重新排列索引,可以获得表达式以赋予每个阶段权力。
