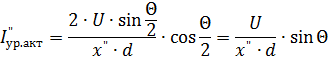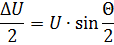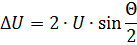发电机并联运行

在发电厂中，总是安装多个涡轮或液压单元，它们在发电机或浪涌的公共母线上并联工作。

因此，发电厂的电力生产是由多台发电机并联工作产生的，这种合作具有许多宝贵的优势。

发电机并联运行：

1.增加了发电厂和变电站设备运行的灵活性，便于发电机、主设备和相应配电设备的预防性维护，所需的储备最少。

2. 提高发电厂的运行效率，因为它可以在机组之间最有效地分配每日负荷计划，从而实现电力的最佳利用并提高效率；在水力发电厂中，可以在洪水期和夏季和冬季枯水期最大限度地利用水流的力量；

3.提高发电厂和消费者供电的可靠性和不间断运行。

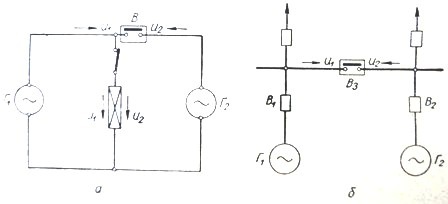
米。 1、发电机并联运行示意图

为了提高产量和改善配电，将许多发电厂联合起来并联运行，形成强大的电力系统。

在正常运行中，发电机连接到公共母线（发电机或过电压）并同步旋转。它们的转子以相同的电角速度旋转

并联运行时，两台发电机两端的瞬时电压必须大小相等，符号相反。

要将发电机与另一台发电机（或网络）并联运行，必须对其进行同步，即根据运行的发电机调节所连接发电机的旋转速度和励磁速度。

并联运行和连接的发电机必须同相，即具有相同的相位旋转顺序。

从图中可以看出。 1、并联运行时，发电机之间是相对连接的，即它们在开关上的电压U1和U2正好相反。相对于负载，发电机组工作一致，即它们的电压U1和U2相匹配。发电机并联运行的这些条件反映在图 1 的图表中。 2.

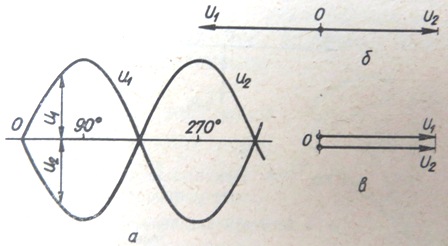
米。 2.发电机并联运行的条件。发电机电压大小相等，相位相反。

同步发电机有两种方法：精同步和粗同步或自同步。

发电机精确同步的条件。

通过精确同步，励磁发电机在达到同步条件时通过开关 B（图 1）连接到网络（母线）——它们的电压瞬时值 U1 = U2 相等

当发电机单独运行时，它们的瞬时相电压将分别相等：

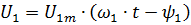
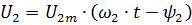
这意味着发电机并联所需的条件。对于启动和运行的发电机，需要：

1.有效电压值相等U1 = U2

2.角频率相等ω1=ω2或f1=f2

3. 相位 ψ1 = ψ2 或 Θ = ψ1 -ψ2 = 0 的电压匹配。

这些要求的准确满足创造了理想条件，其特征在于在发电机接通时，定子均衡电流将为零。然而，应该注意的是，满足精确同步的条件需要仔细调整发电机电压的电压、频率和相位角的比较值。

在这方面，完全满足同步的理想条件实际上是不可能的；它们是近似执行的，有一些细微的偏差。如果不满足上述条件之一，当U2时，电压差将作用在断开的通讯开关B的端子上：

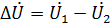
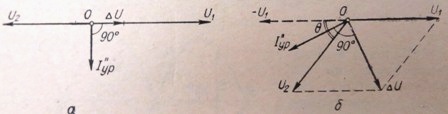
米。 3.偏离精确同步条件的情况的矢量图： a——发电机工作电压不相等； b——角频率不相等。

当开关导通时，在该电位差的作用下，电路中会流过均衡电流，其初始时刻的周期分量为

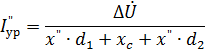
考虑两种偏离图中所示的精确同步条件的情况（图 3）：

1、发电机U1、U2的工作电压不相等，其他条件都满足；

2、发电机电压相同，转速不同，即角频率ω1和ω2不相等，电压相位不匹配。

从图中的图表可以看出。 3、a、电压U1和U2的有效值\u200b\u200b不等导致出现均衡电流I”ur，这几乎是纯感性的，因为发电机和连接线的有源电阻网络非常小，被忽视了。该电流不会产生有功功率浪涌，因此不会在发电机和涡轮机部件中产生机械应力。在这方面，当发电机并联运行时，电压差最多允许 5-10%，在紧急情况下最多允许 20%。

当均方根电压值 U1 = U2 相等，但角频率不同 Δω = ω1 — ω2 ≠ 0 或 Δf = f1 — f2 ≠ 0 时，发电机和网络（或第 2 台发电机的电压矢量) 以随时间变化的特定角度 θ 移动。在这种情况下，发电机 U1 和 U2 的电压相位将不会相差 180°，而是相差 180° —θ（图 3，b）。

在打开的开关 B 的端子处，a 点和 b 点之间，电压差 ΔU 将起作用。与前面的情况一样，可以使用灯泡检测电压的存在，并且可以使用连接在 a 点和 b 点之间的电压表测量该电压的有效值。

如果开关 B 闭合，则在电压差 ΔU 的作用下，会出现均衡电流 I”，与 U2 相关的电流几乎是纯活动的，当发电机并联时，会引起冲击和机械发电机和涡轮机的轴和其他部件中的应力。

在 ω1 ≠ ω2 时，如果滑差为 s0 < 0, l% 且角度 Θ ≥ 10°，则同步完全令人满意。

由于涡轮调节器的惯性，不可能实现角频率 ω1 = ω2 和电压矢量之间的角度 θ 的长期相等，表征发电机定子和转子绕组的相对位置，不会保持不变，而是不断变化；它的瞬时值将是 Θ = Δωt。

在矢量图（图 4）中，最后一种情况将表示为随着电压矢量 U1 和 U2 之间的相位角的变化，ΔU 也将发生变化。此时的电压差ΔU称为冲击电压。

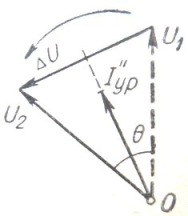
米。 4.频率不等的发电机同步矢量图。

时钟电压的瞬时值 Δu 是发电机电压 u1 和 u2 的瞬时值之差（图 5）。

假设达到有效值U1 = U2相等，则参考时刻ψ1和ψ2的相位角也相等。

然后你可以写

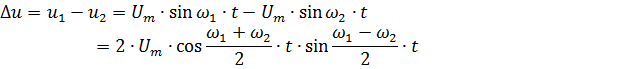
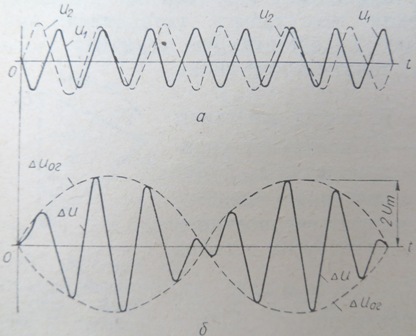
冲击应力曲线如图 1 所示。 5.

节奏电压谐波变化，其频率等于比较频率总和的一半，幅度随时间变化，具体取决于相位角 Θ：

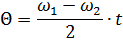
从图中的矢量图。4、对于某一规定的角度θ值，可求出冲击应力的有效值：

米。 5.克服压力的曲线。

考虑到角度 θ 随时间的变化，可以根据冲击应力振幅写出壳的表达式，它给出了应力振幅随时间的变化（图 5，b 中的虚线曲线） ):

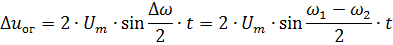
从图中的矢量图可以看出。 4和最后一个方程，冲击应力幅值ΔU从0到2 Um变化。 ΔU 的最大值出现在电压矢量 U1 和 U2（图 4）相位和角度 θ = π 重合的时刻，最小值出现在这些电压的相位相差 180° 且角度 θ = 0 时。节奏曲线的周期等于

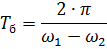
当发电机与大功率系统并联运行时，系统的xc值很小，可以忽略不计（xc≈0），则均衡电流

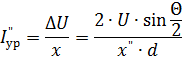
和浪涌电流

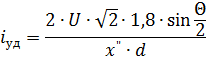
在电流Θ = π 不利合闸的情况下，合闸发电机定子绕组中的浪涌电流可达到发电机端子三相短路浪涌电压值的两倍。

均衡电流的有源分量，从图 1 中的矢量图可以看出。 4等于