单电源的无分支和分支线性电路

如果大量的无源元件与e源一起。 ETC。 c.形成一个电路，它们的互连可以用不同的方式来完成。此类连接有以下典型方案。

元件串联 这是最简单的连接。通过这种连接，相同的电流流过电路的所有元件。根据这种方案，要么将电路中所有的无源元件都连接起来，然后电路将是单路无分支的（图 1.a），要么只连接多路电路的部分元件连接的。

如果n个元件串联，其中流过相同的电流I，则电路两端的电压将等于n个串联元件的电压降之和，即

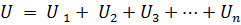
或者：

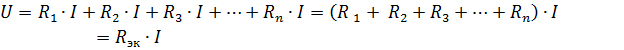
其中 Rek 是等效电路电阻。

因此，串联连接的无源元件的等效电阻等于这些元件的电阻之和......电气方案（图1）1, a) 可以给出一个等效电路（图 1, b），由一个具有等效电阻 Rek 的元件组成

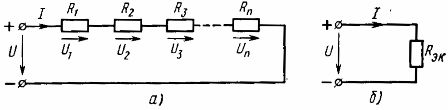
米。 1. 线性元件串联方案(a)及其等效方案(b)

在计算具有给定电源电压和元件电阻的元件串联连接的电路时，根据欧姆定律计算电路中的电流：

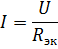
第 k 个元件上的电压降

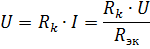
不仅取决于该元件的电阻，还取决于等效电阻Rek，即电路其他元件的电阻。这是元件串联的一个显着缺点。在极限情况下，当电路中任何元件的电阻变为无穷大（开路）时，电路中所有元件中的电流变为零。

由于串联连接时，电路中所有元件中的电流相同，因此元件中的电压降之比等于这些元件的电阻之比：

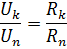
元件的并联连接——这是一种对电路的所有元件施加相同电压的连接。根据并联连接方案，可以连接电路的所有无源元件（图 2，a）或仅连接其中的一部分。每个并联连接的元素形成一个单独的分支。因此，如图 1 所示的元件并联电路。 2、a，虽然是一个简单的电路（因为它只包含两个节点），但它同时是有分支的。

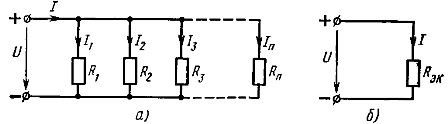
米。 2. 线性元件并联方案(a)及其等效方案(b)

在每个并联支路中，电流

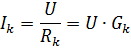
其中 Gk 是第 k 个分支的电导率。

从 基尔霍夫第一定律

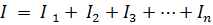
或者

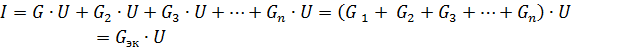
其中 Gec 是等效电路电导。

因此，当无源元件并联时，它们的等效电导等于这些元件的电导之和……等效电导总是大于并联支路任何部分的电导。等效电导率GEK对应于等效电阻Rek = 1 / Gek。

则得到如图所示的等效电路。 2、a，就会有如图所示的形式。 2、b.元件并联电路中未支路部分的电流可由该电路根据欧姆定律求得：

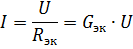
因此，如果电源电压恒定，则随着并联元件数量的增加（导致等效电导率增加），电路未分支部分的电流（电源电流）增加。

从公式

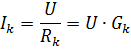
可以看出，每个支路中的电流只取决于该支路的电导，而不取决于其他支路的电导。并联支路模式相互独立是无源元件并联的一个重要优点。在工业装置中，大多数情况下使用电气接收器的并联连接。最明显的例子是用于照明的电灯。

由于在并联连接中，相同的电压被施加到所有元件并且每个支路中的电流与该支路的电导成正比，因此并联支路中的电流之比等于这些支路的电导之比，或成反比与它们的电阻之比：

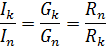
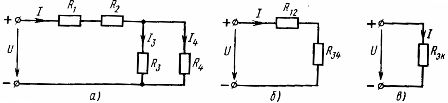
元件的混合连接是串联和并联连接的组合。这样的链可以有不同数量的节点和分支。图中显示了混合连接的示例（图 3，a）

米。 3. 线性单元混合连接方案(a)及其等价方案(b,c)。

要计算这样的电路，必须依次确定电路中仅串联或并联连接的那些部分的等效电阻。在所考虑的电路中，电阻 R1 和 R2 的元件串联连接，电阻 R3 和 R4 的元件并联连接。利用先前获得的电路元件参数与串联和并联连接之间的关系，实际电路可以依次用等效电路代替。

串联元件的等效电阻

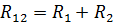
并联元件 R3 和 R4 的等效电阻

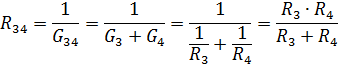
具有元件 R12 和 R34 电阻的等效电路如图 1 所示。 3、乙。 R12和R34串联，等效电阻为

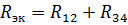
对应的等效电路如图 1 所示。 2，乙。让我们找出该电路中的电流：

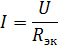
这些是实际电路的电源电流和元件 R1 和 R2 中的电流。要计算电流 I3 和 I4，请确定电阻 R34 电路部分的电压（图 3，b）：

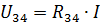
那么电流I3和I4可以根据欧姆定律求得：

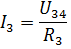
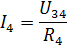
以类似的方式，您可以计算许多其他混合连接无源元件的电路。

对于具有大量电路和e源的复杂电路。 ETC。 c. 这样的等价转换并不总能进行。它们是通过其他方法计算的。