交流电路中的瞬态过程、换向定律、谐振现象

电路的静态操作模式是电路中的参数恒定的模式：电压、电流、电阻等。如果在达到稳态后电压发生变化，电流也会发生变化。从一种稳定状态到另一种稳定状态的转变不会立即发生，而是需要一段时间（图 1）。

在从一种静止状态过渡到另一种静止状态的过程中，电路中发生的过程称为瞬态过程。电路参数的任何突然变化都会发生瞬变。电路工作模式突然改变的时刻被视为初始时刻，相对于它表征电路状态并描述瞬态过程本身。

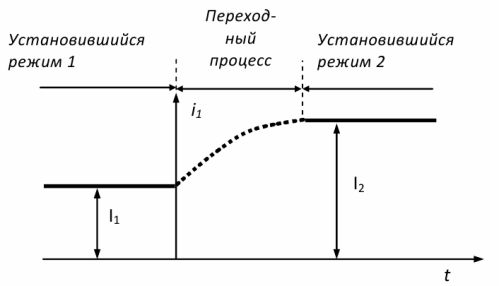
米。 1.交流电路中出现的模式

瞬态过程的持续时间可能非常短，可以在几分之一秒内计算出来，但电流和电压或表征该过程的其他参数可能会达到很大的值。瞬变是由电路中的换向触发的。

换向是开关设备触点的闭合或打开。在分析瞬态时，使用两个换向法则。

换向第一定律：电流。开关前流过电感器的电流等于开关后立即流过同一线圈的电流。这些。电感中的电流不能突然变化。

换相第二定律：开关前电容元件两端的电压等于开关后同一元件两端的电压。这些。电容元件两端的电压不能突变。对于电阻器、电感器和电容器的串联连接，相关性是有效的

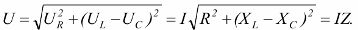
在所考虑的具有相同反应 Xl 和 Xc 的电路中，即所谓的电压谐振... 由于这些电阻取决于频率，因此谐振发生在某个谐振频率 ωо。

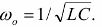
在这种情况下，电路的总电阻是最小的并且是纯有源的。 Z = R，电流有最大值。在 ω ωо 时，负载具有有源电容特性，其中 ω >ωо — 有源电感。

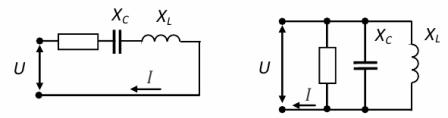
应该注意的是，谐振时电路中电流的急剧增加对应于 Xl 和 Xc 的增加。这些应力会变得比电压大得多。 U 应用于电路端子，因此电压谐振是一种对电气装置很危险的现象。

并联电路元件的支路中的电流相对于总电路电压具有相应的相移。因此，考虑到相移，电路的总电流等于其各个支路电流的总和，并由以下公式确定

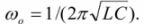
如果电抗 Xl 和 X 相等，在元件并联谐振电流的电路中...谐振电流达到其最大值和最大功率因数 (cosφ = 1)。共振频率的值由以下公式确定

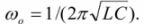
包含 L 和 C 的支路中的电流在谐振时可能大于总电路电流。电感电流和电容电流相位相反，值相等并且相对于电源相互抵消。这些在电路中，能量在电感线圈和电容器之间交换。

电流的接近谐振模式被广泛用于提高用电设备的功率因数。由于电线的卸载、损失的减少、材料和能源的节省，这给出了显着的经济效果。