电路拓扑——基本概念

电路是一组设备（元件）及其连接线，电流可以通过这些连接线流动。电路的所有元件共享 在被动和主动.

有源元件将不同类型的能量（机械能、化学能、光能等）转化为电能。在无源设备中，电能被转换成其他类型的能量。主动元素称为源，被动元素称为消费者或接收者。

在电路理论中，考虑了电气元件的理想化模型。这使得元素的描述尽可能简单。更复杂的真实元素是根据一组理想化元素建模的。

电路中主要的无源元件有电阻器（电阻元件）、电感器（电感元件）和电容器（电容元件）。元件安装在电路中以产生给定值和形状的电压和电流（参见 - 电路及其元件).

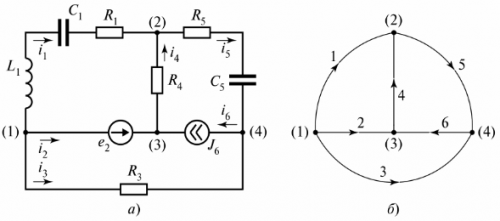
电路由分支和节点组成。 分支 — 这是流过相同电流的电路（电路）的一部分。 一个结 ——三个或更多支路的连接。在电气图上，节点用点表示（图 1）。

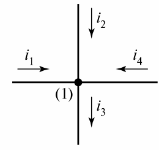
米。 1.定义图中的节点

如有必要，图的节点从上到下从左到右编号。

在图。图 2 显示了电流 iC 流过的阻容支路。

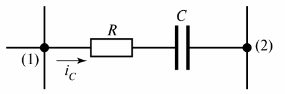
米。 2、阻容支路

可以给出分支的另一个定义——它是两个相邻节点（图 2 中的节点 (1) 和 (2)）之间的电路部分。

链 电路中是否有闭合路径。电路可以通过任何分支闭合，包括电阻等于无穷大的条件分支。

在图。图3显示了由三个支路组成的支路电路。

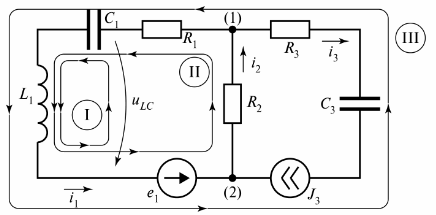
米。 3. 电路有两个电路

该图显示了三个电路，电路 I 由无穷大电阻的支路闭合。该分支表示为电压 tiLC。

对于图一的电路3 可以组成许多由实数或条件分支闭合的循环，但是为了计算电噪声，使用了“独立循环”的概念。独立电路回路的数量始终设置为计算所需的最小值。

独立电路总是闭合的，但分支的电阻不等于无穷大，并且每个独立电路至少包含一个不包含在其他电路中的分支。对于复杂的电路，您可以使用电路图确定独立电路的数量。

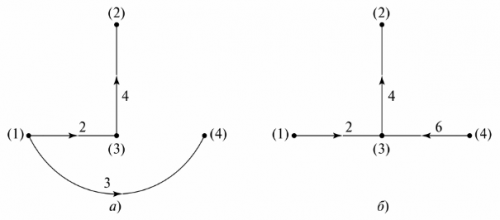
在电路图上 称为电路的条件表示，其中每个分支都由一条线段代替。不显示分支中的项目。例如，在图。图 4 显示了一个分支电路及其示意图。

米。 4、分支电路：a——电路图，b——图

要制作图表的图表，您必须使用分支线连接节点，而无需在其上指定元素。分支被编号，它们上面的电流方向用箭头表示。该图本身没有物理意义，但可以用来判断独立等值线的数量和类型。为此，准备了一个“图形树”。

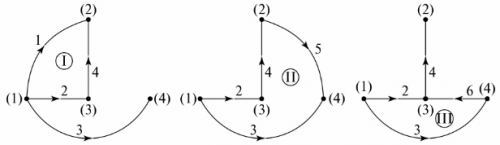
图形树 它表示电路图，其节点通过分支连接，不会产生闭环。显示图形树可能有几个选项。在图。图5示出了图4的电路的两个可能选项。 4.

米。 5. 方案图解树

图树中缺失的分支数等于电路的独立回路数。在这个例子中，这是三个分支，三个独立的循环。独立循环的配置可以通过将图树的节点与图树上未指定的分支顺序连接来获得。例如，对于图 1 中的图树。 5，和独立的轮廓示于图。 6.

米。 6.通过图树确定独立轮廓

选择一个选项来配置独立电路以计算电路是在电路分析期间执行的。您应该选择这样的轮廓，以便计算尽可能简单，即系统中相关方程的数量最少。

拓扑方程建立了电路中电压和电流之间的关系，方程的数量和类型不取决于分支中包含哪些元素。拓扑方程包括由以下组成的方程 根据基尔霍夫定律.