电荷守恒定律

无论世界上发生什么事，宇宙中总有一定的电荷，其大小永远不变。即使电荷由于某种原因在一个地方不复存在，它也肯定会在另一个地方结束。这意味着电荷不会永远消失。

这个事实是由迈克尔法拉第建立和调查的。他曾在他的实验室里竖起一个巨大的空心金属球，在球的外表面连接了一个超灵敏的检流计。球的大小使得在其中放置整个实验室成为可能。

法拉第也是如此。他开始将他可以使用的最多样化的电气设备带入舞会，然后开始进行实验。身处球中，他开始用毛皮摩擦玻璃棒，启动静电机等。但无论法拉第如何努力，球的电荷并没有增加。这位科学家无论如何都没有设法产生电荷。

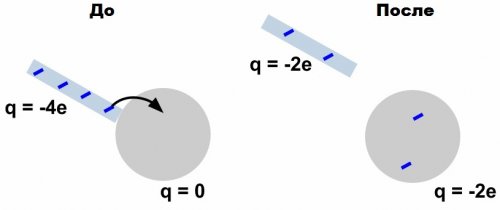
我们理解这一点，因为当你用毛皮摩擦玻璃棒时，即使玻璃棒带正电荷，毛皮也会立即带上相同数量的负电荷，毛皮和玻璃棒上的电荷总和为零.

如果法拉第的实验室出现“额外”电荷，球外的检流计肯定会反映电荷变化的事实，但这种情况并没有发生。节省全部费用。

另一个例子。中子最初是不带电的粒子，但中子可以衰变为质子和电子。尽管中子本身是中性的，也就是说，它的电荷为零，但由于它的衰变而产生的粒子带有相反符号且数量相等的电荷。宇宙的总电荷根本没有改变，它保持不变。

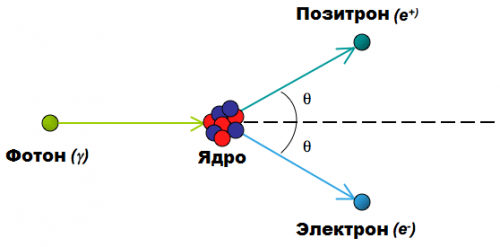
另一个例子是正电子和电子。正电子是电子的反粒子，它带有与电子相反的电荷，本质上是电子的镜像。一旦它们相遇，电子和正电子就会相互湮灭，从而产生伽马量子（电磁辐射），但总电荷再次保持不变。反之亦然（见上图）。

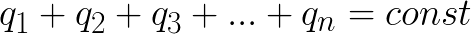
电荷守恒定律表述如下：电封闭系统的电荷代数和守恒。或者像这样：随着物体的每次相互作用，它们的总电荷保持不变。

零件的电荷变化（量化）

电荷有一个不寻常的特性——它总是部分变化。考虑带电粒子。它的电荷可以是，例如，电荷的一份或电荷的两份，减去一份或减去两份。一个基本的（实际存在的最小长寿命粒子）负电荷有一个电子。

电子电荷为 1.602 176 6208 (98) x 10-19 Pendant。该电荷量是最小部分（电荷量）。电荷的微小片段可以从空间中的一个地方移动到另一个地方，但总电荷总是处处守恒，原则上可以用这些微小片段的数量来衡量。

电荷是电场和磁场的来源

值得注意的是，电荷是 电场和磁场……因此，电气方法可以确定其一个或另一个载体上的电荷量。此外，电荷是带电体与电场相互作用的量度。因此，可以认为电是一种与静止电荷（静电、电场）或运动电荷（电流、磁场）相关的现象。