什么是磁动势，霍普金森定律

19 世纪下半叶，英国物理学家约翰·霍普金森和他的兄弟爱德华·霍普金森发展了磁路的一般理论，推导出了一个数学公式，称为“霍普金森公式”或霍普金森定律，它类似于欧姆定律（用于计算电路）。

因此，如果欧姆经典定律在数学上描述了电流和电动势 (EMF) 之间的关系，那么霍普金森定律类似地表达了磁通量与所谓的磁通量之间的关系。 磁动势 (MDF).

结果，原来 磁动势是表征电流产生磁通量能力的物理量。 而这方面的霍普金森定律可以成功地用于磁路的计算，因为磁路中的 MDF 类似于电路中的 EMF。霍普金森定律的发现日期被认为是 1886 年。

磁动势 (MDF) 的大小最初以安培为单位测量，或者，如果我们谈论的是带电流的线圈或电磁铁，那么为了计算方便，请使用其以安匝为单位的表达式：

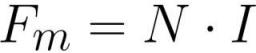
其中：Fm 是线圈中的磁动势 [安培 * 匝]，N 是线圈的匝数 [匝]，I 是线圈每匝中的电流量 [安培]。

如果您在此处输入磁通量值，则磁路的霍普金森定律将采用以下形式：

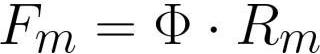
其中：Fm为线圈中的磁动势[安培*匝]，F为磁通量[韦伯]或[亨利*安培]，Rm为磁通导体的磁阻[安培*匝/韦伯]或[转/亨利]。

霍普金森定律的文字表述原来是这样的：“在无支路的磁路中，磁通量与磁动势成正比，与总磁阻成反比”。即这个定律决定了电路中磁动势、磁阻和磁通量之间的关系：

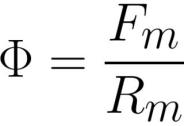
此处：F为磁通量[韦伯]或[亨利*安培]，Fm为线圈中的磁动势[安培*转]，Rm为磁通导体的磁阻[安培*转/韦伯]或[转/亨利]。

这里需要注意的是，实际上磁动势（MDF）与电动势（EMF）有一个根本的区别，在于没有粒子直接在磁通量中移动，而电流是在磁通量的作用下产生的EMF 采用带电粒子的运动，例如金属线中的电子。不过，MDS的思路有助于解决磁路计算的问题。

例如，考虑一个无分支磁路，它包括一个横截面积为 S 的磁轭，在整个长度上相同，磁轭的材料具有磁导率 mu。

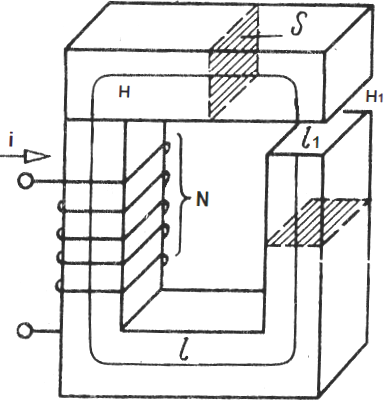
轭中的间隙 - 不同的材料， 磁导率 哪个mu1。放置在磁轭上的线圈包含 N 匝，电流 i 流过线圈的每一匝。我们将磁场循环定理应用于磁轭的中心线：

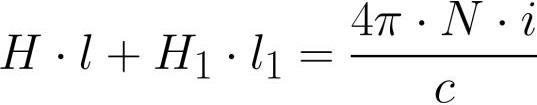
其中：H为磁轭内磁场强度，H1为间隙内磁场强度，l为磁轭感应中心线长度（无间隙），l1为间隙长度。

由于磁轭内部和间隙内部的磁通量具有相同的值（由于磁感应线的连续性），所以在写出 Ф = BS 和 В = mu * H 后，我们将更详细地写下磁场强度，并将其代入上述公式后：

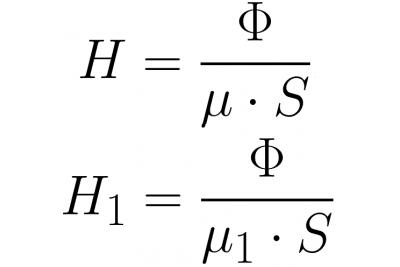
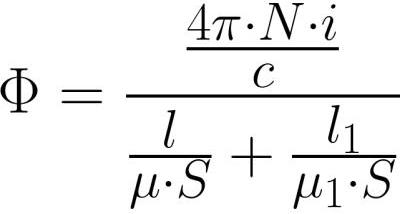
很容易看出，就像电路欧姆定律中的 EMF 一样，MDS

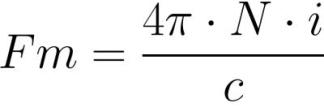
这里起着电动势和磁阻的作用

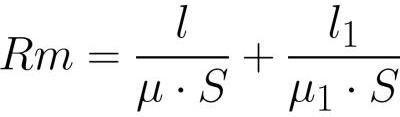
阻力的作用（以此类推 与经典欧姆定律).