电路的时间常数——它是什么以及用在什么地方

周期性过程是自然界固有的：白天之后是夜晚，暖季被寒冷取代等。这些事件的周期几乎是恒定的，因此可以严格确定。此外，我们有权声称，作为示例引用的周期性自然过程不会贬值，至少就人的寿命而言是这样。

然而，在技术领域，尤其是在电气工程和电子领域，并非所有过程都是周期性的和连续的。通常，一些电磁过程先增大后减小。通常物质只限于振荡的开始阶段，没有时间真正加快速度。

在电气工程中，您经常会发现所谓的指数瞬态，其本质是系统只是努力达到某种平衡状态，最终看起来像静止状态。这种转变可以增加或减少。

外力首先使动力系统失去平衡，而后又不妨碍该系统自然恢复到原来的状态。最后一个阶段是所谓的过渡过程，其特点是有一定的持续时间。此外，系统失衡的过程也是一个具有特征持续时间的瞬态过程。

无论如何，暂态过程的时间常数，我们称之为它的时间特性，它决定了这个过程的某个参数将在多少时间后变化时间«e»，即它会增加或减少约2.718倍与初始状态相比。

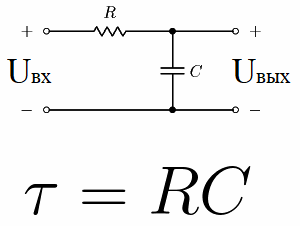
例如，考虑一个由直流电压源、电容器和电阻器组成的电路。这种电阻与电容串联的电路称为RC积分电路。

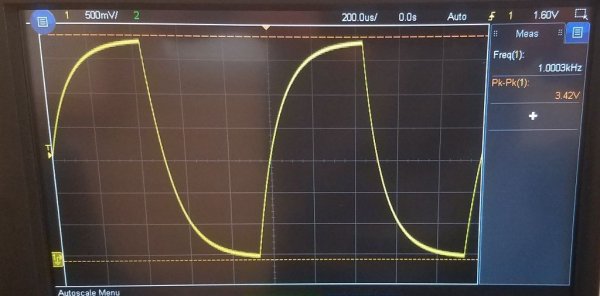
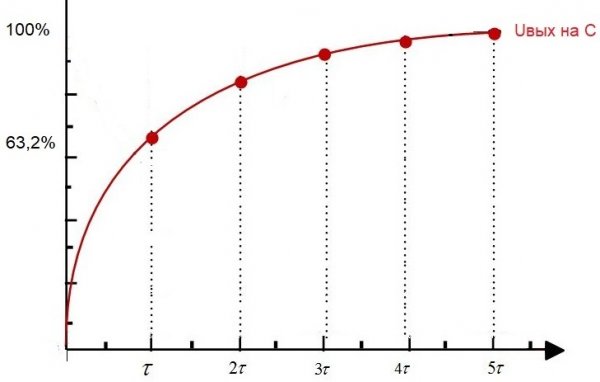
如果在初始时刻为这样的电路供电，即在输入端设置恒定电压 Uin，则 Uout——电容器中的电压将开始呈指数增长。

在时间 t1 之后，电容器电压将达到输入电压的 63.2%。所以，从初始时刻到t1的时间间隔就是这个RC电路的时间常数。

该链常数称为“tau”，以秒为单位，并由相应的希腊字母表示。在数值上，对于 RC 电路，它等于 R * C，其中 R 的单位是欧姆，C 的单位是法拉。

当必须切断（抑制）较高频率并必须通过较低频率时，集成 RC 电路在电子设备中用作低通滤波器。

实际上，这种过滤的机制是基于以下原则。对于交流电，电容器充当容性电阻，其值与频率成反比，即频率越高，电容器的电抗（欧姆）越低。

因此，如果交流电通过 RC 电路，那么，就像在分压器的臂上一样，电容器两端会下降一定的电压，与通过的电流频率下的电容成正比。

如果已知输入交变信号的截止频率和幅值，那么设计者在RC电路中选择这样的电容和电阻就不难了，使得最小（截止）电压（对于截止频率 - 频率的上限）落在电容器上，因为电抗与电阻器一起进入分压器。

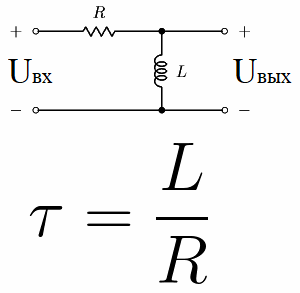
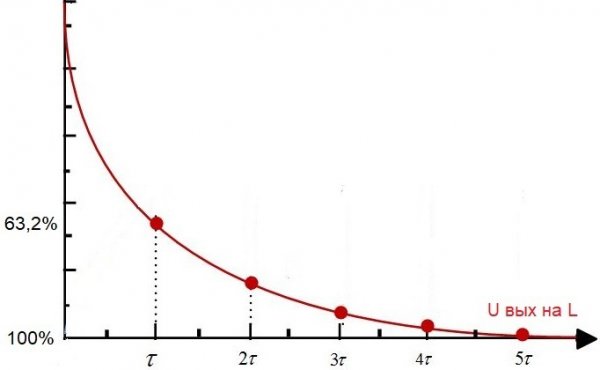
现在考虑所谓的微分电路。它是由一个电阻和一个电感串联组成的电路，RL电路。它的时间常数在数值上等于 L / R，其中 L 是以亨利为单位的线圈电感，R 是以欧姆为单位的电阻器的电阻。

如果将来自电源的恒定电压施加到此类电路，经过一段时间 tau 后，线圈电压将相对于 U in 降低 63.2%，即完全符合该电路的时间常数值.

在 AC 电路（交流信号）中，当必须切断（抑制）低频并且忽略高于（高于截止频率 - 频率下限）的频率时，LR 电路用作高通滤波​​器。所以，线圈的电感越大，频率就越高。

与上面讨论的 RC 电路的情况一样，这里使用分压器原理。通过 RL 电路的更高频率的电流将导致电感 L 上的电压降更大，就像作为分压器和电阻器一部分的电感电阻一样。设计者的任务是选择这样的 R 和 L，以便恰好在边界频率处获得线圈的最小（边界）电压。