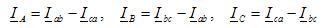三相电路的计算

链 三相交流电 由三相电源、三相用电器和它们之间的通讯线路组成。

对称三相电源可以表示为三个单相电源，它们以相同的频率和相同的电压工作，并且相位角为 120°。这些来源可以星形或三角形连接。

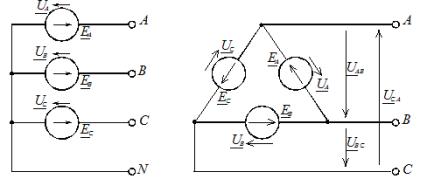
星形接法时，用相线的有条件始端连接三根线状导体A、B、C，相线的端部连在一点，称为电源的中性点（三相发电机或变压器）。可在该点接零线N，电源星形连接图如图1，a。

米。 1、电源相线连接图：a——星形； b — 三角形

线路和中性导体之间的电压称为相位，线路导体之间的电压称为线路（有关更多详细信息，请参见此处 - 线电压和相电压).

V 综合形式 相电压表达式的条目是：

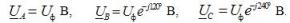
星接时对应的线电压：

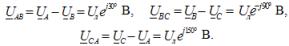
这里 Uf 是电源的相电压模量，Ul 是线电压模量。在对称的三相系统中，当源相星形连接时，这些电压之间存在关系：

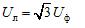
当相位以三角形连接时，相位电源串联在一个闭环中（图 1，b）。

三根线性导线 A、B、C 从源相互组合点引出，连接到负载。从图1b中可以看出，相源的输出端连接的是线性导线，因此，当源的相位以三角形连接时，相电压等于线性。在这种情况下，没有零线。

负载可以连接到三相电源。就大小和性质而言，三相负载可以是对称的和不对称的。

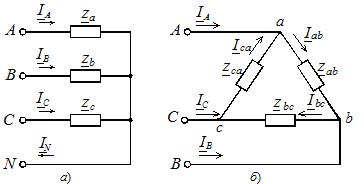
在负载对称的情况下，三相的复电阻相同，如果这些电阻不同，则负载不平衡。无论电源连接方案如何，负载相位都可以通过星形或三角形相互连接（图 2）。

米。 2.负载相连接图

星形连接可以带或不带中性线（见图 2，a）。没有中性线消除了负载电压与电源电压的刚性连接，并且在非对称相位负载的情况下，这些电压彼此不相等。为了区分它们，我们同意在电源电压和电流的字母指定索引中使用大写字母，在负载特定参数中使用小写字母。

分析三相电路的算法取决于负载连接方案、初始参数和计算目的。

双节点法用于确定没有中性线的不平衡星形连接负载的相电压。根据这种方法，计算从确定电源中性点和负载之间的电压 UN 开始，称为中性点偏差电压：

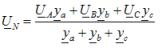
其中 ya, yb, yc — 复数形式的相应负载阶段的允许值

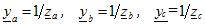
不平衡负载各相间的电压可通过以下表达式找到：

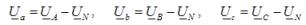
在负载不平衡的特殊情况下，在没有中性导体的情况下，其中一个负载相发生短路，中性点偏置电压等于短路相电源的相电压发生。

负载闭合相上的电压为零，而另外两个在数值上等于线电压。例如，假设 B 相发生短路。这种情况下的中性点偏置电压为 UN = UB。那么负载上的相电压：

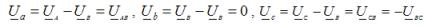
负载中的相电流，它们也是任何类型负载的线导体电流：

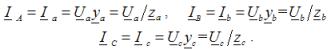
在计算三相电路的任务中，考虑了用星形连接三相用电设备的三种选择：在三相有用电设备的情况下连接到中性线，在没有用电设备的情况下连接到中性线。相位的连接，并且在其中一个负载相位中没有带短化合物的中性线连接......

在第一个和第二个版本中，电源的相应相电压位于负载相上，负载中的相电流由上述公式确定。

在第三个版本中，负载相位的电压不等于电源的相位电压，并且使用相关性来确定

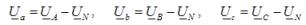
两个未短路相中的电流根据欧姆定律确定为相电压除以相应相阻抗的分数。短路电流使用基于以下公式确定 基尔霍夫第一定律编译为负载的中性点。

对于上述 B 相短路示例：

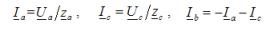
对于每一类负载，三相有功功率和无功功率分别等于各相有功功率和无功功率之和。要确定这些相功率，您可以使用表达式

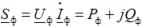
其中 Uf,Azf 是负载相电压和耦合电流的复数； Pf、Qf——负载阶段的有功功率和无功功率。

三相有功功率：P=Pa+Pb+Pc

三相无功功率：Q=Qa+Qb+Vc

三相视在功率：

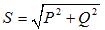
当消费者通过三角形连接时，电路采用图 2，b 所示的形式。在这种模式下，平衡电源的相位连接是无关紧要的。

在负载相上检测电源线之间的电压。负载中的相电流使用以下方法确定 电路部分的欧姆定律Azf = Uf /zf，其中Uf——负载中的相电压（对应电源的市电电压）； zf 为负载对应相的总电阻。

线性导体中的电流由基于基尔霍夫第一定律的相电流确定，对于图 2、b 所示电路的每个节点（点 a、b、c）：