电场中的电子

电子在电场中的运动是电气工程中最重要的物理过程之一。图 让我们看看这是如何在真空中发生的。让我们首先考虑一个电子在均匀电场中从阴极移动到阳极的例子。

下图显示了一种情况 电子 以可忽略的小初始速度（趋于零）离开负电极（阴极）并进入 在均匀电场中存在于两个电极之间。

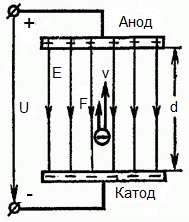
在电极上施加恒定电压U，电场具有相应的强度E。电极之间的距离等于d。在这种情况下，一个力 F 将从场的一侧作用在电子上，它与电子的电荷和场的强度成正比：

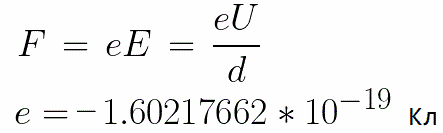
由于电子带负电荷，该力将针对场强矢量 E。因此，电子将被电场沿该方向加速。

电子所受的加速度与作用在其上的力 F 的大小成正比，与电子的质量 m 成反比。由于场是均匀的，给定图片的加速度可以表示为：

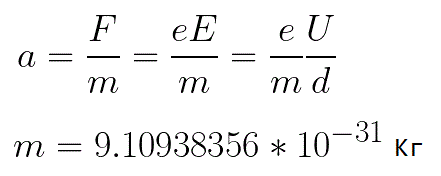
在这个公式中，电子的电荷与其质量的比率是电子的比电荷，一个物理常数的量：

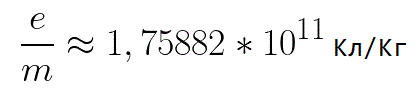
所以电子处于加速电场中，因为初速度v0的方向与场侧力F的方向重合，因此电子作匀速运动。如果没有障碍物，它将沿着电极之间的路径 d 以一定的速度 v 到达阳极（正极）。在电子到达阳极的那一刻，其动能将相应地等于：

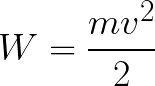
由于电子沿着整个路径 d 被电场力加速，因此它获得了这种动能，这是作用在电场一侧的力所做的功的结果。这项工作等于：

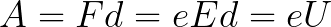
则电子在场中运动所获得的动能可由下式求得：

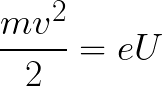
也就是说，在电位差为U的点之间加速电子无非是场力的功。

在这种情况下，为了表示电子的能量，使用“电子伏特”这样的测量单位很方便，它等于电子在 1 伏特电压下的能量。并且由于电子电荷是恒定的，那么 1 伏特也是一个恒定值：

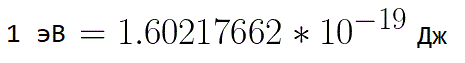
根据前面的公式，您可以轻松确定电子在加速电场中移动时其路径上任意一点的速度，只需知道它在加速时通过的电势差：

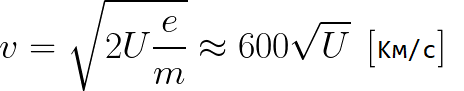
正如我们所见，电子在加速场中的速度仅取决于其路径的终点和起点之间的电势差 U。

想象一下，电子开始以可以忽略不计的速度远离阴极，阴极和阳极之间的电压为 400 伏。在这种情况下，在到达阳极的那一刻，它的速度将等于：

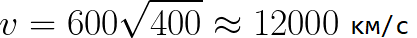
也很容易确定电子行进电极之间的距离 d 所需的时间。由静止匀加速运动，求平均速度为最终速度的一半，则在电场中加速飞行的时间为：

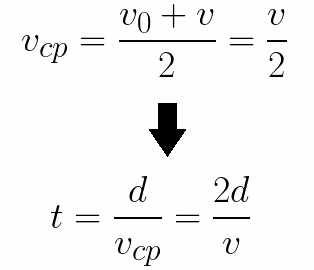
现在让我们考虑一个电子在减速均匀电场中移动的例子。也就是说，电场的方向和以前一样，但电子开始向相反的方向移动——从阳极到阴极。

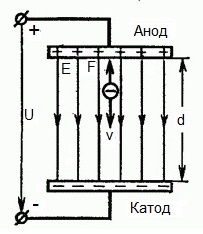
假设电子以某个初始速度 v 离开阳极，并开始朝阴极方向移动。在这种情况下，从电场一侧作用在电子上的力 F 将针对从阴极到阳极的电场强度矢量 E。

它会开始降低电子的初始速度，也就是说，场会使电子减速。这意味着在这些条件下的电子将开始均匀且均匀地缓慢移动。情况描述如下：“电子在减速电场中运动”。

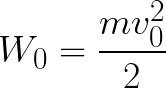
从阳极开始，电子开始以非零动能运动，在减速过程中动能开始减少，因为能量现在被消耗在克服场作用在电子上的力上。

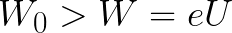
如果电子离开阳极时的初始动能立即大于场必须消耗的能量以加速电子从阴极移动到阳极（如第一个示例），则电子将行进一段距离 d，尽管有刹车，但最终会到达阴极。

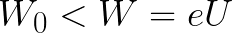
如果电子的初始动能小于这个临界值，那么电子就不会到达阴极。在某一点它会停止，然后开始均匀加速运动回到阳极。结果，场会将停止过程中消耗的能量返回给它。

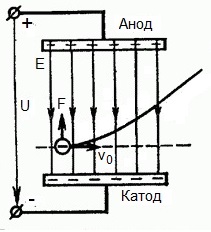
但是，如果一个电子以速度 v0 在电场作用区内以直角飞行呢？显然，该区域场侧的力是针对电子从阴极到阳极的，即与电场强度矢量E相反。

这意味着现在电子有两个运动分量：第一个 - 速度为 v0 垂直于场，第二个 - 在场侧指向阳极的力的作用下均匀加速。

事实证明，电子飞入作用域后，沿着抛物线轨迹运动。但飞出场作用区后，电子将继续沿直线轨迹作惯性匀速运动。