交流电感

考虑一个包含电感器的电路，并假设电路（包括线圈线）的电阻非常小，可以忽略不计。在这种情况下，将线圈连接到直流电源会导致短路，众所周知，电路中的电流会非常大。

当线圈连接到交流电源时，情况就不同了。在这种情况下，不会发生短路。由此可见。电感器对通过它的交流电有什么抵抗力。

这种抵抗的本质是什么，它是如何形成的？

要回答这个问题，请记住自感现象…线圈中电流的任何变化都会导致其中出现自感电动势，从而阻止电流变化。自感 EMF 的值与线圈的电感值以及其中电流的变化率。但是由于交流电连续变化线圈中连续出现的自感电磁辐射对交流电产生电阻。

了解发生在交流电路与电感器，见图表。图 1 显示的曲线分别表示电路中的标记、线圈中的电压和线圈中出现的自感电动势。让我们确保图中的构造是正确的。

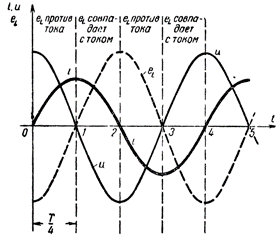
带电感的交流电路

从 t = 0 时刻开始，即从观察电流的初始时刻开始，它开始快速增加，但随着它接近最大值，电流增加的速率减小。在电流达到最大值的瞬间，其变化率瞬间变为零，即电流停止变化。然后电流开始缓慢，然后迅速下降，并在第二个季度后下降到零。这四分之一周期内电流的变化率，从子弹开始递增，当电流变为零时达到最高值。

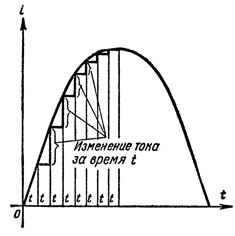
电流随时间变化的性质，取决于电流的大小

图 2. 电流随时间变化的性质，具体取决于电流大小

从图2的结构可以看出，当电流曲线经过时间轴时，电流在短时间T内的增加幅度大于电流曲线达到峰值时的同一时间段内的增加幅度。

因此，无论电路中电流的方向如何，电流的变化率都随着电流的增大而减小，随着电流的减小而增大。

可见，当电流变化率最大时，线圈中的自感电动势必然最大，而当电流停止变化时，则电动势减小为零。事实上，在图上，第一季度自感eL的电动势曲线，从最大值开始，下降到零（见图1）。

在下一个季度期间，电流从最大值减小到零，但其变化率逐渐增加，并且在电流等于零的时刻最大。相应地，该四分之一期间的自感电动势再次出现在线圈中，逐渐增加并变为最大值，直到电流变为零。

然而，自感电动势的方向发生了相反的变化，第一季度电流的增加被第二季度的减少所取代。

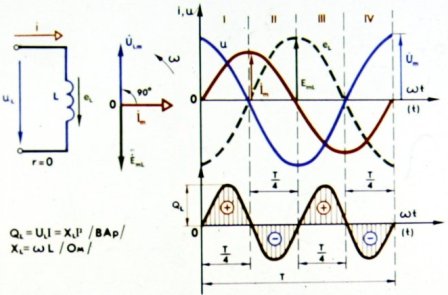
电感电路

继续进一步构建自感电动势曲线，我们确信在线圈电流变化期间，线圈中的自感电动势将完成一个完整的变化周期。它的方向是确定的楞次定律：随着电流的增加，自感电动势将与电流方向相反（周期的第一和第三季度），随着电流的减少，相反，它与方向重合（该期间的第二和第四季度）。

因此，交流电本身引起的自感电动势阻止了它的增加，相反，它在下降时保持不变。

交流电感

现在让我们转向线圈电压图（见图 1）。在此图中，线圈端电压的正弦波显示为与自感电动势的正弦波相等且相反。因此，线圈两端的电压在任何时刻都与线圈中产生的自感电动势大小相等且方向相反。该电压由交流发电机产生，用于终止 EMF 自感应电路中的动作。

因此，在连接到交流电路的电感器中，电流流动时会产生电阻。但由于这种电阻最终会引起线圈的电感，所以称为感性电阻。

感应电阻用 XL 表示，以电阻形式测量，单位为欧姆。

电路的电感电阻越大，越大电流源频率电路电源和更大的电路电感。因此，电路的电感电阻与电流的频率和电路的电感成正比；由公式 XL = ωL 确定，其中 ω — 由乘积 2πe 确定的圆频率... — n 中的电路电感。

欧姆定律对于包含电感电阻的交流电路，声音因此：电流量与电压成正比，与 NSi 的电感电阻成反比，即I = U / XL，其中I和U为有效电流和电压值，xL为电路的感性电阻。

考虑线圈中电流变化的图表。自感电动势和终端电压，我们注意到它们 vValues 的变化不及时重合。换句话说，电流、电压和自感 EMF 正弦曲线对于所考虑的电路来说彼此之间存在时间偏移。在交流技术中，这种现象通常称为相移。

如果两个变量按照相同的规律（在我们的例子中是正弦曲线）以相同的周期变化，同时在正向和反向方向上达到最大值，并且同时减小到零，那么这些变量具有相同的相位，或者，正如他们所说，相匹配。

例如，图 3 显示了相位匹配的电流和电压曲线。我们总是在仅由有源电阻组成的交流电路中观察到这种相位匹配。

在电路中包含电感电阻的情况下，电流和电压相位，如图 1 所示。 1 不匹配，即这些变量之间存在相移。这种情况下的电流曲线似乎滞后于电压曲线四分之一的周期。

因此，当交流电路中加入电感时，电路中电流和电压之间会发生相移，电流同相滞后于电压四分之一周期……这意味着最大电流出现四分之一达到最大电压后的时间段。

自感电动势与线圈电压反相，滞后电流四分之一周期，此时电流、电压的变化周期，以及线圈的电动势自感不会改变，并且保持等于为电路供电的发电机电压的变化周期。这些值变化的正弦性质也得以保留。

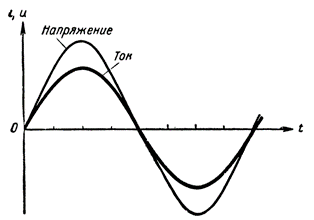
有源电阻电路中电流和电压的相位匹配

图 3. 有源电阻电路中电流和电压的相位匹配

现在让我们了解具有有源电阻的交流发电机负载与具有感性电阻的负载之间的区别。

当交流电路只包含一个有源电阻时，电流源的能量被有源电阻吸收，加热电线.

交流电感

当电路不包含有源电阻（我们通常认为它为零）而仅由线圈的电感电阻组成时，电流源的能量不会用于加热电线，而只会用于产生自感电动势，也就是说，它变成了磁场的能量......然而，交流电的大小和方向都在不断变化，因此，磁场线圈随着电流的变化而不断变化。在第一季度期间，当电流增加时，电路从电流源接收能量并将其存储在线圈的磁场中。但是，一旦达到最大值的电流开始下降，它就会以自感应电动势存储在线圈磁场中的能量为代价来维持。

因此，电流源在周期的第一季度将其部分能量提供给电路，并在第二季度从充当电流源的线圈接收回能量。换句话说，仅包含电感电阻的交流电路不消耗能量：在这种情况下，电源和电路之间存在能量波动。相反，有源电阻吸收从电流源传输给它的所有能量。

与欧姆电阻不同，电感器相对于交流电源而言是无效的，即reactive... 因此，线圈的感应电阻也称为电抗。

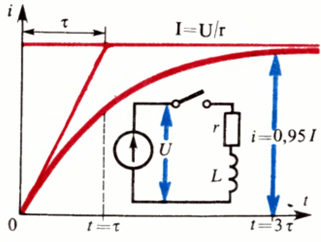
闭合包含电感的电路时的电流上升曲线 — 电路中的瞬变.